Établir des prévisions statistiques
Objectif du chapitre
« Il est difficile de faire des prédictions, en particulier sur l’avenir ».
Niels Bohr
Dans ce chapitre, nous allons étudier quelques-uns des outils statistiques les plus utilisés en pratique pour établir une prévision en marketing.
Le type de question que l’analyste marketing est amené à se poser peut-être :
Quelle est la tendance des ventes et quels sont les facteurs qui peuvent l’influencer ?
Comment le prix affecte-t-il la demande ?
Comment la publicité affecte-t-elle les ventes ?
Quelles sont les caractéristiques d’un produit qui sont les plus susceptibles de plaire aux clients ?
Cependant, ce chapitre ne vous donnera pas de boule de cristal.
Nous allons simplement, à travers des outils statistiques éprouvés, utiliser des données historiques d’entreprise pour établir des prévisions.
En d’autres termes, nous allons nous fier au passé pour tenter de prévoir le futur.
Si ce travail est important, il ne constitue en fait que la moitié d’un travail prédictif efficace. En effet, pour mener son analyse, l’entreprise doit aussi réaliser un travail qualitatif sur les aspects économiques de son marché et de son environnement :
Quelle est ma part de marché ?
À quelle étape de cycle...
La régression linéaire
Principe
La régression est probablement l’outil statistique le plus utilisé pour établir des prévisions. Le but de la régression est d’estimer la relation qu’il existe entre deux ou plusieurs variables.
Si le modèle a une seule variable explicative, il s’agit d’une régression linéaire simple. Dans le cas où le modèle à plusieurs variables explicatives, nous parlerons d’une régression linéaire multiple.
Il est possible de faire des régressions linéaires avec des variables numériques ou catégorielles.
Enfin, toutes les régressions ne sont pas linéaires, selon la relation qu’il existe entre les données, il pourra s’agir de régressions non linéaires.
Cette méthode doit son nom à Francis Galton, mathématicien, statisticien et sociologue anglais qui fut un des premiers à l’utiliser, notamment pour tenter de prédire la taille d’un enfant à l’âge adulte en fonction de la taille de ses parents en 1888.

Francis Galton 1822 - 1911
Aujourd’hui, la régression linéaire est utilisée dans toutes sortes de domaines : dans la finance, dans le domaine de la santé, dans les études économiques, sociologiques et bien entendu, en marketing.
La régression linéaire a même été utilisée par un professeur d’économie de l’université de Priceton, Orley Ashenfelter, pour prédire la qualité d’un vin.
Il s’agit probablement de l’algorithme le plus utilisé en data sciences/machine learning.
Régression linéaire - Intuition

Cet exemple est un graphique en nuage de points représentant sur l’axe des abscisses, la taille en centimètres d’individus et sur l’axe des ordonnées leur poids en kilo.
Même s’il existe des personnes plus lourdes ou plus légères que la moyenne, il est probable qu’il y ait une relation entre le poids et la taille des individus.
Si nous tentons de tracer une droite représentant la tendance de ce graphique, plusieurs points seront en dessous de cette droite, d’autres seront au-dessus et quelques points seulement se retrouveront...
La régression linéaire multiple
Concept
La régression linéaire multiple (ou multivarié) utilise les mêmes principes que la régression linéaire simple, mis à part que dans ce cas on utilisera deux ou plusieurs variables explicatives.
Le but étant d’utiliser plus de variables afin d’obtenir une meilleure information sur le comportement, une variable d’intérêt et ses prédicteurs, afin de mieux prendre en compte la complexité du modèle et de réaliser de meilleures prévisions.
L’équation d’une régression linéaire multiple peut être écrite :
y = a1x1 + a2x2..... anxn + b
Avec :
y est la variable dépendante, aussi appelée variable expliquée. Il s’agit de la variable dont le modèle va tenter d’expliquer le mieux possible la variabilité.
X1, x2, xn sont les variables indépendantes, aussi appelées prédicteurs ou variables explicatives. Il s’agit des données qui vont servir au modèle pour tenter d’expliquer la variabilité de y.
a1, a2, an sont les coefficients directeurs associés à chacune des différentes variables indépendantes.
b est l’ordonnée à l’origine de la droite.
Contrairement au nuage de points en deux dimensions qui représente...
Régression linéaire, concept avancé
Déterminer les variables indépendantes importantes : la P-valeur
Une fois la régression multiple lancée et les différents coefficients calculés, une question naturelle vient à l’esprit :
Quelles sont les variables indépendantes qui sont réellement utiles pour établir une prédiction ?
Après tout, si vous choisissez le nombre de matchs gagnés par votre équipe de foot local au cours d’une période comme variable indépendante, vous vous attendez à ce que cette variable ait peu ou pas d’effet sur votre prévision des ventes.
Pour chaque variable indépendante, une P-valeur comprise entre 0 et 1 est calculée. Toute variable indépendante avec une P-valeur inférieure ou égale à 0,05 est considérée comme utile pour prédire la variable dépendante.
Au seuil de 0,05, la P-valeur d’une variable indépendante a 95 % (1- 0,05) de chance d’apporter un pouvoir prédictif au modèle.
Ainsi, plus la P-valeur est petite, plus le pouvoir prédictif de la variable indépendante est élevé.
Dans la version française d’Excel, la P-valeur a été traduite par Probabilité.
Pourquoi un seuil de 0,05 ?
Le choix d’un seuil...
La régression linéaire avec variables catégorielles
Concept
Une variable catégorielle aussi appelée variable qualitative est tout simplement une variable sur laquelle il n’est pas possible de faire un calcul. Cela peut être par exemple :
-
Le genre : femme/homme
-
Des données géographiques : Est/Nord/Sud/Ouest
-
Des nationalités
Contrairement aux variables numériques, pour faire une régression linéaire avec des variables catégorielles, il va falloir utiliser une technique spéciale : la technique de la variable muette (dummy variable). P54a
Comme il n’est pas possible de faire des calculs avec des variables catégorielles, nous allons utiliser un code qui ressemble au code binaire.
|
Femme/Homme |
|
|
|
Nom |
Homme |
Femme |
|
Elena |
0 |
1 |
|
Bob |
1 |
0 |
Dans la colonne Homme, nous avons attribué la valeur 1 à la ligne Bob pour signifier qu’il s’agit d’un homme et dans la colonne Femme, nous avons attribué la valeur 1 à la ligne Elena pour signifier qu’il s’agit d’une femme.
Il est possible de simplifier le tableau précédent de la manière suivante : (p54b)
|
Femme/Homme |
|
|
Nom |
Femme |
|
Elena |
1 |
|
Bob |
0 |
Elena a la valeur 1 dans la colonne Femme, et Bob a la valeur 0, signifiant qu’il ne s’agit pas d’une femme (et donc c’est forcément un homme).
Le principe est le même avec quatre variables catégorielles. (p55)
|
Région habitée |
|||
|
Nom |
Est |
Ouest |
Nord |
|
Elena |
0 |
0 |
1 |
|
Bob |
0 |
0 |
0 |
Dans cet exemple, Elena habite dans la région Nord et Bob n’habite pas dans la région Est ni dans la région Ouest ni dans la région Nord. Il habite donc forcément dans la région Sud.
Application avec Excel
Un magasin de jouets investit régulièrement dans des campagnes de publicité internet et papier. Récemment, le magasin a particulièrement centré ses campagnes publicitaires sur deux modèles de jouets.
Le directeur du magasin souhaiterait déterminer lequel des deux médias est le plus susceptible d’améliorer son chiffre d’affaires pour chacun des deux modèles de jouet. Il souhaiterait en outre estimer quel serait son chiffre d’affaires probable...
Pour aller plus loin : les régressions non linéaires
Dans l’exemple de l’onglet reg_linéaire du fichier reg_non_lineaire.xlsx, la droite de régression linéaire a un coefficient de détermination R2 de 0,8711.
Même si le modèle explique bien la relation entre les semaines et le chiffre d’affaires, en regardant attentivement la forme du nuage de points, il apparaît qu’une équation de type logarithmique serait plus pertinente.
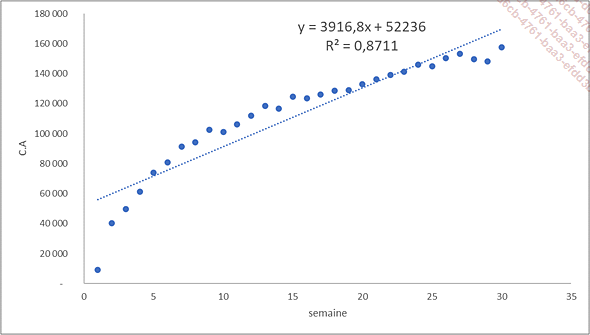
Pour réaliser la régression logarithmique :
Sélectionnez les cellules C1 :D31, au niveau du ruban, allez dans l’onglet Insertion, dans le groupe Graphiques, cliquez sur Insérer un nuage de points (X,Y) ou un graphique en bulles.
Sélectionnez le graphique Nuage de points.
Dans l’onglet Création de graphique du ruban, au niveau du groupe Dispositions du graphique, cliquez sur Ajouter un élément graphique.
Dans Courbe de tendance, sélectionnez Autres options de la courbe de tendance. Le volet Format de courbe de tendance apparaît à droite de l’écran.
Dans le volet Format de courbe de tendance, allez dans Options de courbe de tendance. Cochez Logarithmique et Afficher l’équation sur le graphique, Afficher le coefficient de détermination (R2) sur le graphique.
Vous retrouverez ce graphique dans l’onglet...
L’analyse conjointe
Intuition
L’analyse conjointe est une technique statistique utilisée dans les études de marché pour tenter de déterminer comment les potentiels consommateurs (appelés répondants) apprécient les différents attributs (fonctionnalité, fonction, avantages) qui constituent un produit ou un service individuel.
L’objectif de l’analyse conjointe est de déterminer quelle combinaison d’un nombre limité d’attributs a le plus d’influence sur le choix ou les préférences des répondants.
Un ensemble contrôlé d’attributs (services, design, option sur un produit…) est présenté aux répondants.
Après avoir montré à un consommateur plusieurs produits et lui avoir demandé de classer ces profils de produit, l’analyste peut utiliser une analyse conjointe complète pour déterminer l’importance relative des divers attributs.
L’analyse conjointe permet à l’analyste marketing de déterminer les caractéristiques du produit qui déterminent en moyenne la préférence d’un consommateur.
Par exemple, lors de l’achat d’une nouvelle voiture, qu’est-ce qui compte le plus pour le client :
-
La marque ?
-
Le prix ?
-
La consommation de carburant ?
-
Le style ?
-
Le type moteur ?
Cette technique est originaire de la psychologie mathématique et a principalement été développée par le professeur de marketing Paul Green à la Wharton School de l’université de Pennsylvanie.
En pratique, l’analyse conjointe est une régression multiple utilisant des variables catégorielles.
L’analyse conjointe en pratique
Le but de cette étude conjointe est de déterminer le rôle que cinq attributs jouent dans l’influence de la préférence d’un consommateur pour un aspirateur.
Les quatre attributs (et leurs niveaux) jugés pertinents pour le consommateur sont les suivants :
-
Le design (A, B ou C)
-
Des options (1, 2 ou 3)
-
Le prix (60, 70, 80 €)
-
La garantie (oui...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations