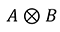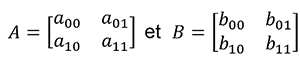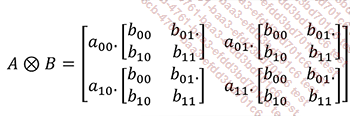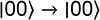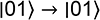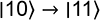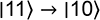Définition des circuits quantiques
Introduction
La revue d’effectifs des principales portes quantiques étant réalisée, nous pouvons à présent réfléchir à les assembler pour former des circuits quantiques visant à assurer une certaine sortie. Le premier exemple de circuit quantique sera autour des états de Bell. C’est en général le premier exemple choisi, car d’une part il fait écho à la violation des inégalités de Bell, fondamentale en physique quantique comme vu dans la première partie. D’autre part, le circuit est relativement simple, car composé de seulement deux portes quantiques élémentaires.
Mais avant de détailler plus avant, il nous faut préciser le mode de calcul impliquant qubits et matrices de transformation dans un circuit donné.
Produit tensoriel
On distingue deux cas :
-
Deux portes logiques sont positionnées en série (ci-dessous à gauche).
-
Deux portes logiques sont positionnées en parallèle (ci-dessous à droite).
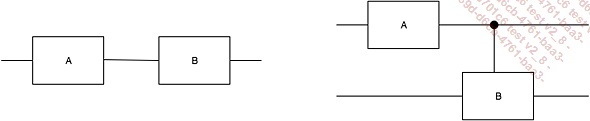
Illustration 1 : à gauche un montage en série ; à droite un montage en parallèle
1. Montage en série
Dans un montage en série, rien de bien compliqué. On a une porte après l’autre, la seconde porte prenant en entrée le qubit sortant de la première porte.
Si A et B sont les portes d’Hadamard, on a alors :
-
en sortie de la porte A. Puis :
-
en sortie de la porte B.
On a procédé au calcul matriciel en séquence pour obtenir le résultat précédent. Il en va bien autrement quand les deux portes sont montées en parallèle.
2. Produit de Kronecker
Le produit de Kronecker ou produit tensoriel consiste en l’opération suivante entre deux matrices (ici, de dimension 2). Il se représente avec un symbole constitué d’une croix inscrite dans un cercle, comme dans cet exemple :
Considérons les deux matrices suivantes A et B :
Alors :
On voit donc que deux portes quantiques en parallèle sont représentées par un produit tensoriel de deux matrices de dimension 2 et que l’on va alors obtenir une matrice de dimension 4. Plus généralement...
Les états de Bell
1. Explications
Avant de présenter le (petit) schéma permettant la production des états de Bell, revenons sur les inégalités de Bell étudiées dans un des chapitres précédents. En substance, les inégalités de Bell permettent de conclure que l’intrication quantique s’accompagne forcément par le viol de certaines inégalités dites de Bell. Or, l’intrication la plus facilement atteignable est celle des états de Bell qui justement viole les inégalités de Bell. Il ne s’agit pas ici de démontrer ce résultat, mais d’expliquer comment on atteint ces états de Bell qui correspondent à des états quantiques intriqués.
Le schéma quantique générant les états de Bell est constitué d’une porte de Hadamard suivi d’une porte NOT. Ci-dessous la représentation de ce schéma :
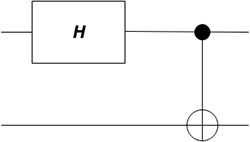
Illustration 2 : représentation du schéma de la production des états de Bell
Pour rappel, la porte NOT effectue les transformations suivantes en dimension 4 :
2. Initialisation
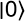 en entrée du schéma ce qui
peut donc s’interpréter comme un état
en entrée du schéma ce qui
peut donc s’interpréter comme un état 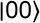 .
.Quelle est la sortie de la porte de Hadamard H ? On applique la transformation étudiée précédemment :...
Téléportation quantique
1. Explications
Comme nous l’avons vu, l’intrication quantique permet d’obtenir un état quantique partagée par deux bits quantiques. Si on décide d’éloigner les deux bits quantiques concernés, que l’on nomme A et B, les deux bits quantiques resteront intriqués. Par contre, l’intrication ne permet pas en soi un transfert immédiat d’informations. C’est un mécanisme nécessaire, mais non suffisant. En effet, ce transfert d’information se nomme en général téléportation quantique. Et ce phénomène utilise largement l’intrication quantique et notamment les états de Bell précédemment étudiés.
2. Scénario de téléportation
|
1. |
On envisage deux personnages Alice (A) et Bob (B) chacun lié symboliquement à deux bits quantiques intriqués A et B selon un des états de Bell. |
|
2.
 |
On envisage les deux qubits A et B intriqués
selon l’état de Bell
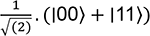 . . |
|
3.
 |
Alice a connaissance d’un état quantique
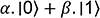 c’est-à-dire le vecteur c’est-à-dire le vecteur  . . |
|
4.
 |
L’idée est de téléporter
vers Bob cette information portée par l’état quantique
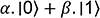 . . |
3. Schéma quantique de téléportation
Classification des problèmes à résoudre et complexité
1. L’informatique classique face à l’informatique quantique
a. Complexité des problèmes à résoudre
Pour le moment, nous avons vu comment fonctionne l’informatique quantique et comment réaliser des premiers algorithmes quantiques utilisant des portes quantiques. Toutefois, on perçoit encore mal l’intérêt de l’informatique quantique. En effet, son intérêt se place forcément dans l’idée que l’informatique quantique serait parfois plus performante que l’informatique classique sur certains problèmes.
Nous détaillerons donc une manière de classer des problèmes, notamment de recherche opérationnelle, selon leurs complexités. Certaines classes de problèmes sont aujourd’hui impossibles à résoudre avec l’informatique classique. Trouver ou approcher une solution de certaines instances de ces problèmes supposerait de laisser tourner des algorithmes classiques pendant des centaines d’années. L’informatique quantique constitue donc un espoir (théorique) d’atteindre des solutions exactes ou approchées sur des instances de problèmes qui échappent à nos capacités actuelles.
b. Parallélisation quantique ou la puissance...
Typologie des problèmes
1. Contexte
L’émergence d’une nouvelle discipline comme l’informatique quantique pose la question des problèmes qu’elle peut aider à résoudre. Comme évoqué précédemment, on qualifie un algorithme de résolution avec sa complexité. Cette notion nous permet donc de catégoriser les problèmes que les algorithmes considérés participent à résoudre.
Commençons par détailler cette notion de complexité des algorithmes.
2. La complexité
En informatique classique, il a fallu à un moment donné quantifier la performance d’un algorithme en fonction des données en entrée du problème à résoudre. Il en va de même en informatique quantique. Cette quantification se nomme complexité.
a. Première approche
Il s’agit donc de caractériser cette complexité en fonction de la nature des entrées de l’algorithme selon le problème à résoudre. En effet, plus les données en entrée correspondent à des grandeurs conséquentes, plus l’algorithme mettra a priori du temps pour atteindre la solution.
Prenons par exemple l’algorithme qui consiste à parcourir un tableau d’une seule dimension. Il s’agit pour l’algorithme de parcourir tout le tableau en lisant chaque valeur dans chaque case du tableau.
-
S’il y a trois cases dans le tableau, l’algorithme procédera à trois itérations.
-
S’il y a n cases, l’algorithme procédera à n itérations.
Pour noter cette complexité, on utilise la notation de Landau qui utilise un O (« grand O »). Ainsi, pour notre premier exemple, la complexité associé est : O(n).
Ceci se prononce comme suit : « Grand O de n ». On voit donc que l’on cherche à établir le temps de calcul de l’algorithme face à un problème donné en fonction des données en entrée.
S’il s’agit maintenant de parcourir un tableau à deux dimensions de tailles n et m, par exemple n=2 et m=3. Il faut donc 6 itérations pour passer sur chaque case. Il faut donc de manière générale...
Vers la suprématie quantique ?
1. Introduction
On ressent à ce stade que même si un algorithme quantique ne fournit en définitive qu’une seule sortie et donc qu’un seul résultat, la superposition qu’il utilise permet d’accéder à une sorte de parallélisation des calculs qui permet d’accélérer les choses.
Il n’y a certes rien de magique. À un problème donné, il s’agit de trouver un algorithme à même d’être exécuté sur un ordinateur quantique. On ne peut pas prendre un algorithme d’informatique classique et se dire qu’il s’exécuterait plus vite sur un ordinateur quantique. Ce n’est malheureusement pas aussi simple.
Si, pour un problème donné, on est capable, d’une part, de trouver un algorithme quantique, et d’autre part, de voir cet algorithme quantique donner de meilleurs résultats que le meilleur algorithme classique appliqué au même problème, alors on parle contextuellement de suprématie quantique.
2. L’algorithme quantique de Shor
Dans les faits, un exemple célèbre d’algorithme quantique permet d’accéder à un balbutiement de suprématie quantique. Il s’agit de l’algorithme quantique de Shor portant le nom du mathématicien américain...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations