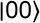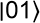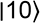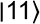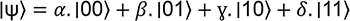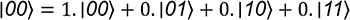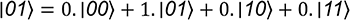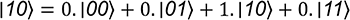Le bit quantique
Vers le bit quantique
1. Du bit au bit quantique
Le bit quantique dont l’écriture est habituellement simplifiée en qubit, voire qu-bit, ou encore qbit est l’unité de base de stockage en informatique quantique. C’est l’équivalent du bit de l’informatique classique. En effet, dans un ordinateur, l’ensemble des informations qui circulent sont réductibles à des séquences de « 0 » et de « 1 ». Pour le codage de l’information d’abord, puis lors de son traitement qui utilise intensivement des portes logiques. Ces portes sont réalisées matériellement avec des dizaines voire des centaines de millions de transistors qui composent nos ordinateurs. De manière symétrique, nous étudierons par la suite les portes quantiques de l’informatique quantique.
Dorénavant, nous prendrons l’écriture qubit pour désigner un bit quantique. Dans la littérature ou dans la presse informatique, le qubit est parfois présenté comme « un bit qui peut valoir à la fois 0 et 1 ». On reconnaît ici le principe de superposition quantique largement étudié précédemment.
C’est effectivement ce principe qui sous-tend la définition d’un qubit qui a comme valeur éligible à la mesure (écrites...
Définition vectorielle du bit quantique
Détaillons un peu plus encore les différentes valeurs possibles d’un qubit et ses possibles variations. Pour cela, nous allons utiliser une approche vectorielle.
1. Exemple à un qubit
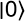 et
et 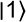 en explicitant
les coefficients
en explicitant
les coefficients 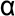 et
et 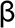 dans leurs écritures vectorielles respectives.
dans leurs écritures vectorielles respectives.-
; correspondant donc au vecteur (1 0).
-
; correspondant donc au vecteur (0 1).
On peut alors tenter d’écrire les formes vectorielles quand on a deux qubits.
2. Exemple à deux qubits
Quand on a deux qubits, on a évidemment quatre valeurs possibles mesurables qui sont les suivantes :
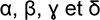 :
:On peut donc alors et comme précédemment déterminer les vecteurs associés à chaque valeur mesurable :
-
Correspondant donc au vecteur (1 0 0 0)
-
Correspondant donc au vecteur (0 1 0 0)
-
Correspondant donc au vecteur (0 0 1 0)
-
Correspondant donc au vecteur (0 0 0 1)
Les quatre vecteurs ainsi définis forment une base vectorielle de dimension 4 nous permettant d’écrire la combinaison linéaire décrivant n’importe quel état quantique avant mesure.
Pour des raisons pratiques, les vecteurs ont été écrits ici horizontalement. Rien n’empêche toutefois de les écrire verticalement.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations