La complexité algorithmique
Introduction
La complexité algorithmique n’a de complexe que le nom. C’est une notion plutôt intuitive à comprendre qui fait référence à une des caractéristiques fondamentales des algorithmes qui peut se résumer en ces deux questions :
-
Quand cet algorithme va-t-il se terminer ?
-
De combien de mémoire (RAM, ROM) cet algorithme a-t-il besoin pour fonctionner ?
Répondre à ces questions, c’est découvrir le degré de complexité d’un algorithme. Autrement dit, il s’agit de mesurer la quantité de ressources nécessaires pour que l’algorithme atteigne son but. Cela permet également de comparer les performances des algorithmes, dans la mesure où ils ont le même objectif. Cela évite aussi d’attendre plusieurs secondes ou minutes, voire plusieurs heures qu’un algorithme se termine alors qu’il ne le fera jamais ou du moins qu’il va mettre un temps beaucoup trop grand avant de se terminer. Il faut en ce sens avoir une idée du nombre de calculs que l’algorithme effectuera. Autrement dit, il faut avoir une idée de la complexité spatiale et temporelle de notre algorithme. Ces deux notions ne concernent pas uniquement les boucles infinies, bien que leur utilisation soit un exemple classique où l’on risque de saturer la mémoire...
La complexité spatiale
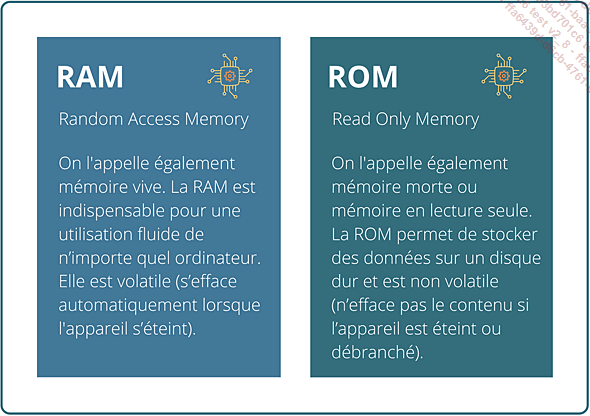
La complexité spatiale fait référence à l’espace en mémoire que nécessite un algorithme pour s’exécuter. Pour rappel, un ordinateur a une mémoire RAM et une mémoire ROM limitées.
La mémoire RAM, ou mémoire vive, est la mémoire de fonctionnement quand l’ordinateur est alimenté électriquement. Elle fournit des données au processeur de l’ordinateur de manière rapide. Il existe plusieurs types de RAM, qui diffèrent par leur taille et par leur rapidité d’exécution :
-
La mémoire centrale, qui se trouve au niveau de la carte mère.
-
La mémoire cache, qui est plus petite et aussi plus rapide.
-
Le registre, qui est la mémoire la plus rapide et la plus petite. Elle se trouve dans le processeur.
La mémoire ROM, ou mémoire morte, est une mémoire qui ne s’efface pas lorsque l’ordinateur n’est plus alimenté électriquement. Elle est plus lente que la mémoire vive, mais bien plus volumineuse. On distingue aussi différents types de ROM (PROM, EPROM, EEPROM…).
Quand on allume un ordinateur ou un smartphone pour la première fois, des logiciels et programmes ont déjà été installés, par exemple le système d’exploitation. Par conséquent...
La complexité temporelle
La complexité temporelle permet de calculer le temps qu’un algorithme mettra à se terminer. Plusieurs algorithmes peuvent résoudre le même problème, mais ils n’auront pas tous la même efficacité temporelle. Autrement dit, ils ne nécessiteront pas le même nombre d’opérations élémentaires pour s’exécuter, ce qui aboutira logiquement à un temps d’exécution différent. Prenons l’exemple d’un itinéraire pour se rendre en vacances. Cinq moyens de transport sont envisageables :
-
voiture
-
train
-
bus
-
avion
-
pied
Chacune de ces options est en quelque sorte un algorithme différent qu’on pourrait ranger dans une catégorie "algorithmes de déplacement". Certes, dans l’absolu, l’avion est le moyen de transport le plus rapide ; mais, en fonction du contexte (grève, etc.), c’est-à-dire du chemin à parcourir, certains moyens de transport ont une efficacité temporelle plus grande que d’autres. Par exemple, si vous allez voir votre voisin d’en face, la voiture est une perte de temps. Si vous vous rendez sur un autre continent, l’avion est indéniablement le plus rapide.
Notation
On utilise la lettre O majuscule pour désigner l’ordre de complexité d’un algorithme. Le nombre d’entrées à traiter est noté n. Voilà un résumé des complexités algorithmiques les plus utilisées :
-
O(1) : complexité en temps constant. Elle ne varie pas en fonction des données.
-
O(log(n)) : complexité logarithmique.
-
O(n) : complexité linéaire comme celle de la factorielle.
-
O(n2) : complexité quadratique.
-
O(10n) : complexité exponentielle.
Un algorithme pouvant effectuer plusieurs types d’opérations, sa complexité algorithmique varie en fonction de l’opération qu’il exécute.
Exemple de la recherche d’un élément dans une liste
Les algorithmes de tri et de recherche sont d’excellents exemples pour comprendre la complexité algorithmique. Prenons l’exemple d’une liste qui contient un nombre x de chiffres. Il s’agit de trouver la position d’un élément dans la liste.
La méthode naïve consiste à parcourir la liste en utilisant une boucle. À chaque tour, on vérifie si la valeur de l’élément à la position n correspond à l’élément qu’on recherche. Si c’est le cas, on arrête le processus, sinon on continue en cherchant l’élément à la position n+1, jusqu’à atteindre le dernier élément. La complexité de l’algorithme vaut au maximum le nombre de processus à exécuter si on devait parcourir la liste en entier.
Peut-on faire mieux ? Oui ! On peut par exemple commencer par diviser la liste en deux listes de taille identique. On parcourt ensuite chaque sous-liste à tour de rôle et on cherche l’élément. Avec un peu de chance, on aura besoin de parcourir qu’une seule des deux sous-listes, ce qui réduit la complexité maximale de l’algorithme de moitié.
Peut-on faire mieux ? Oui. Il y a par exemple l’algorithme de la recherche...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
