Le programme du lycée
Le programme officiel de spécialité NSI
Le programme officiel de l’enseignement de spécialité numérique et sciences informatiques (NSI) est paru au Journal officiel du 20 septembre 2019. Il est consultable à cette adresse : https://www.education.gouv.fr/pid285/bulletin_officiel.html?cid_bo=138157
Le ministère conseille largement la démarche projet et la met au centre de l’enseignement de l’informatique afin de permettre aux élèves de s’approprier les notions vues en cours en développant des projets applicatifs. Ce livre met largement en avant cette pédagogie et chaque chapitre propose plusieurs projets du plus simple au plus complexe pour que chacun puisse trouver un défi à son niveau.
Le programme proposé par le ministère est assez vaste, car il couvre des matières très diverses de l’informatique. Voici les différents thèmes proposés que nous avons déjà traités dans les chapitres précédents :
-
types
-
conditions
-
tuples
-
liste et indexation
-
langages de programmation
Les thèmes suivants ne sont pas abordés dans notre livre, car ils ne sont pas propres au langage Python et ils vont être normalement traités avec d’autres environnements et d’autres langages :
-
base de données
-
architecture web
-
réseau
-
systèmes...
L’interaction homme-machine
Nous présentons comment construire une application fenêtrée. Ce type d’application est différent des applications console. Les applications console exécutent un programme, font ce qu’elles doivent faire et s’arrêtent lorsqu’elles ont fini. Elles peuvent interagir avec l’utilisateur en lui demandant d’entrer une information au clavier, mais cela est prévu dans le code. Le flux de traitement se déroule de manière linéaire du début jusqu’à la fin.
Les applications fenêtrées sont interactives, on peut cliquer sur un bouton, cocher une case, faire défiler l’affichage en faisant glisser un ascenseur ou ne rien faire ! Il n’est pas possible de connaître le flux de contrôle de ce type de programme, car ce sont les actions de l’utilisateur qui vont finalement déclencher telle ou telle fonction.
L’affichage visuel permet à l’utilisateur d’interagir avec le programme et la machine, d’où le nom d’interaction homme-machine (IHM). Le terme anglophone est graphical user interface (GUI). Une application fenêtrée qui ne reçoit pas d’évènements de l’utilisateur reste en attente, elle ne consomme pas de ressources CPU.
Nous allons présenter les différents composants servant à construire une IHM et ensuite nous vous présenterons quelques projets. Nous avons choisi la librairie Tkinter, la raison principale étant qu’elle est installée par défaut avec Python et qu’étant assez ancienne, beaucoup d’informations sont disponibles à son sujet sur Internet. Elle n’est pas la librairie la plus high-tech et sa syntaxe n’est pas toujours homogène d’un élément à l’autre. Cependant, elle est facile d’accès et remplit 98 % des besoins, elle convient donc à l’essentiel de vos usages. Il existe beaucoup d’autres librairies d’interface comme PyQt, PySide ou encore wxPython… L’avantage indéniable est que toutes ces librairies, y compris Tkinter, sont multiplateformes, PC ou Mac, ainsi votre code fonctionnera sur n’importe quelle machine.
1. Le nerf de la guerre : les IHM
Vous ne vous en rendez pas compte, mais chaque librairie d’IHM se rattache souvent à un système et à un langage. Par exemple pour macOS, on trouve la librairie Cocoa écrite en Objective C. Pour Android, c’est la bibliothèque UIControls accompagnée du langage Java. Sur PC, on trouve les composants graphiques .NET en C#. Pourquoi tant d’offres ? En fait, vous n’en êtes pas tout à fait conscient même si vous êtes les premiers utilisateurs : l’interface d’un téléphone ou d’un ordinateur portable fait partie des premiers critères de confort. Ainsi, les librairies graphiques représentent une zone de compétition intense du développement informatique, car il faut fournir aux utilisateurs l’interface la plus conviviale possible.
Le copier-coller n’a pas toujours existé ! De même, la touche...
Les tracés scientifiques
Nous vous proposons d’utiliser la librairie Matplotlib pour tracer des fonctions en Python. Cette librairie a dû être installée si vous avez suivi le chapitre Installer l’environnement Python, sinon veuillez vous y reporter.
1. Tracer des fonctions
La correction de cet exercice est disponible en téléchargement depuis l’onglet Compléments avec le nom de fichier : PLT_tracer des fonctions_Presentation.py.
Le tracé d’une fonction sur les calculatrices scientifiques ou sur les ordinateurs requiert l’échantillonnage de la fonction sur un certain nombre de points. Ainsi, comme nous le ferions pour un tracé sur une feuille, nous choisissons certaines valeurs de x et nous calculons les valeurs f(x) correspondantes afin de déterminer certains points (x,f(x)) de la courbe. Le tracé est effectué en reliant ces différents points un à un.
Nous allons tracer la courbe f(x) = x². Pour cela, il faut d’abord choisir plusieurs valeurs pour les abscisses. Pour simplifier les choses, nous pouvons choisir des valeurs entre deux bornes avec un intervalle régulier comme X = [-1, 0, 1, 2, 3, 4]. Ensuite, il suffit de calculer les valeurs de f(x) correspondantes et de les stocker dans une liste Y = [1, 0, 1, 4, 9 ,16]. Ainsi, pour tracer l’échantillonnage de la fonction y=x², nous écrivons :
import matplotlib.pyplot as plt
X = [-1, 0, 1, 2, 3, 4]
Y = [1, 0, 1, 4, 9 ,16]
plt.plot(X,Y)
plt.show() Voici le tracé obtenu :
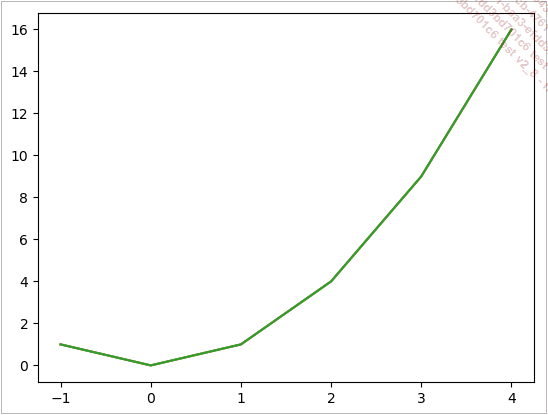
Si vous oubliez la commande plt.show(), la fenêtre de graphique ne s’ouvrira pas, même si votre code est correct. Ce n’est pas un bogue, c’est un oubli !
La ligne import matplotlib.pyplot as plt permet d’importer la sous-librairie Pyplot de Matplotlib et de l’utiliser sous le nom plt dans le code. Cela évite de devoir taper à chaque fois matplotlib.pyplot.mafonction(), ce qui est un peu long. Vous pouvez donc utiliser : plt.mafonction().
Nous reconnaissons la position des points que nous avons calculés car ils correspondent aux endroits sur la courbe où se situent des cassures. Entre deux points, le logiciel dessine un segment, ce qui donne cet air "cabossé" à la courbe. Notre échantillonnage est médiocre, car nous avons pris vraiment peu de points. Ceci dit, cela est suffisant pour reconnaître la forme de la parabole.
Pour générer une liste d’abscisses de manière automatique, nous pouvons utiliser une fonction très pratique de la librairie Numpy : numpy.arange(debut, fin, pas).
Il suffit alors de calculer les valeurs f(x) pour chaque abscisse x disponible et de les stocker dans la liste Y :
import matplotlib.pyplot as plt
import numpy
X = numpy.arange(-1,5,0.1)
Y = []
for x in X :
Y.append(x**2)
plt.plot(X,Y)
plt.show() Cette fois-ci, le graphique obtenu est d’une qualité impressionnante. La courbe est lisse et correspond parfaitement à la courbe attendue. Dans le tableau X se trouvent 60 valeurs d’abscisse de -1 à 5 par pas de 0.1. Cela semble suffisant pour obtenir un tracé de qualité.
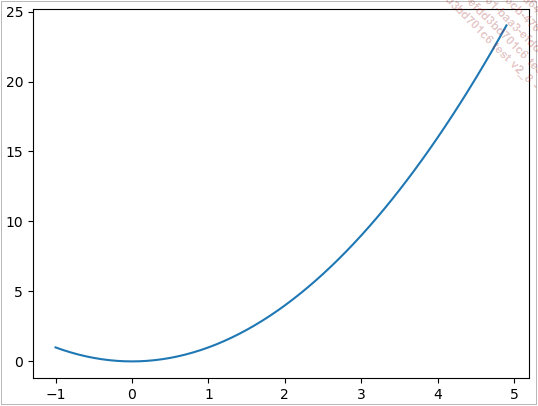
Le graphique manque...
La complexité des algorithmes
Nous vous proposons une boîte à outils assez riche pour étudier la complexité des algorithmes. Pour avoir enseigné cette matière pendant plusieurs années, il est possible d’avoir quelques repères permettant de traiter ces questions avec une certaine précision. Sans cette approche, les exercices d’analyse de complexité ressemblent malheureusement à une émission du Juste Prix où il s’agit de lancer une proposition en espérant faire mouche.
En espérant démystifier cette notion de complexité qui ne mérite pas cette réputation de science obscure et élitiste, nous vous proposons des descriptions assez complètes dans les exercices de ce chapitre. Nous étudions uniquement la complexité dans le pire cas, cette notion étant la plus simple à mettre en œuvre. D’autres approches de l’évaluation de la complexité existent, comme la complexité en moyenne. Vous ne devez pas ajouter des complexités dans le pire cas avec des complexités en moyenne. Même si elles partagent la même notation en O, elles sont rattachées à des concepts différents.
1. La notion de complexité
Cette thématique est chère à l’histoire de l’informatique, car historiquement elle a été au centre du cassage du code de cryptage Enigma utilisé par l’armée allemande durant la Seconde Guerre mondiale. L’équipe anglaise menée par Alan Turing, un des pionniers et des pères de l’informatique, a réussi à la fois à créer un des premiers ordinateurs et à concevoir un programme de décryptage suffisamment rapide. Alan Turing, génie de l’informatique théorique et technique, contrairement à Marc Zuckerberg diplômé de psychologie, ne connaîtra pas une fin heureuse. Peu d’hommes étaient capables à l’époque de mettre en place de tels outils de décryptage. Dans une époque de conflits permanents entre les blocs de l’Est et de l’Ouest où les affaires d’espionnage et de contre-espionnage battaient leur plein, un esprit comme Turing représentait un problème pour les deux camps.
Pourquoi s’intéresse-t-on à la complexité ? Si l’on prend le problème de la cryptographie, la réponse est évidente. Si l’on dispose d’un ordinateur d’une puissance inimaginable, on peut décrypter n’importe quel message. En effet, les méthodes de cryptage sont aujourd’hui connues et utilisées par tout un chacun. Le seul secret restant est la clé utilisée dans la méthode de codage. Ainsi, n’importe quel ordinateur peut générer des clés au hasard et essayer de déchiffrer un message avec. La principale contrainte est finalement le temps passé à effectuer les essais.
Lorsque nous calculons x²+3x+6 avec un ordinateur, quel est le temps utilisé par ce calcul ? La réponse est difficile, car cela dépend du processeur. Certains ont des fréquences...
Les méthodes de tri
Trier un ensemble de nombres est un problème historique de l’informatique, qui a fait phosphorer les cerveaux de beaucoup de chercheurs dans les années 1960 à 1990. Nous avons vu pourquoi trier est important : lorsqu’une base de données est triée, on peut rechercher à l’intérieur avec un temps logarithmique, et non plus linéaire. Le gain de performances est phénoménal et cela ne requiert qu’un unique tri préalable.
Dans le cas d’un dictionnaire de langue, par exemple, les mots sont triés par ordre alphabétique. Si ce n’était pas le cas, il faudrait parcourir toutes les pages du dictionnaire pour une recherche, personne ne ferait cela.
Inconsciemment, nous associons la recherche dans une grande base de données (le dictionnaire) à la notion de tri, cela semble naturel.
Les algorithmes de tri sont pédagogiquement très intéressants pour plusieurs raisons :
-
Ils ne nécessitent pas une connaissance approfondie du langage : nous avons besoin de savoir manipuler les boucles, les conditions et les lectures/écritures dans une liste/un tableau. Ainsi, après quelques heures de programmation, nous pouvons commencer à coder des méthodes de tri.
-
Ils ne requièrent pas la connaissance de librairies supplémentaires, comme les accès disque ou les affichages graphiques. Un simple print() peut servir à déboguer et à afficher les résultats.
-
Le problème du tri nécessite 10 secondes pour être expliqué et autant pour être compris. On dit parfois des meilleurs jeux de société que ce sont ceux avec les règles les plus simples qui sont souvent les plus amusants.
-
Ils sont variés : il existe au moins huit méthodes de tri classiques, plus les méthodes exotiques propres à des situations particulières. Intellectuellement, cela développe un esprit d’analyse et d’organisation qui permet d’envisager l’idée que plusieurs méthodes sont disponibles pour résoudre un même problème.
-
Les algorithmes de tri font en général autour de 20 lignes. Un algorithme a donc une chance d’être traité sur une séance de 2 h. Ainsi, avec deux séances de 2 h, on peut espérer qu’un groupe de deux élèves arrive à produire entre un et trois algorithmes.
Dans cette section, vous travaillez avec les tableaux Numpy et n’utilisez que les accès indexés sur ces structures. La librairie Numpy permet d’initialiser aléatoirement des tableaux très rapidement, ce qui sera utile pour vos tests. L’accès et l’écriture indexée de ces tableaux sont en temps constant, ce qui sera pratique lorsque vous calculerez des complexités.
Les fonctions de manipulation des listes en Python sont des boîtes noires dont on ne connaît pas les complexités sous-jacentes. Il faut donc, pour ces exercices, vous en priver car elles brouilleraient les évaluations des complexités des méthodes de tri.
Les tableaux stockant des résultats seront alloués au démarrage...
Projets


La correction de ce projet est disponible en téléchargement depuis l’onglet Compléments sous le nom de fichier : NSI PR k plus proches voisins.py.
L’algorithme des k plus proches voisins est un algorithme d’apprentissage qui permet de prédire la catégorie d’un élément à partir d’éléments de caractéristiques et de classes déjà connues.
Supposons que nous étudions un problème avec trois catégories : trois types de fleurs ou trois familles de microbes… Pour chacune de ces catégories, nous extrayons deux paramètres (x,y) : comme la taille et le poids, ou l’âge et le taux d’un marqueur sanguin. En partant d’échantillons servant de vérité terrain, nous allons essayer de prédire la catégorie de nouveaux échantillons.
Pour pouvoir travailler, nous construisons tout d’abord nos échantillons de référence virtuels en tirant aléatoirement des groupes d’échantillons :
import matplotlib.pyplot as plt
import random
points= []
N = 50 # nombre d'échantillons par catégorie
Centre = [ (20,20), (80,50), (10,80)]
for categorie in range(3):
for i in range(N):
x = random.normalvariate(Centre[categorie][0],20)
y = random.normalvariate(Centre[categorie][1],20)
if 0 < x < 100 and 0 < y < 100 :
points.append((x,y,categorie))
c2 = ('darkred','darkgreen','lightblue' )
for point in points:
x,y,cat = point
plt.scatter(x,y, s=20, c=c2[cat], marker='o')
plt.show() Nous générons à partir du centre de chaque catégorie 50 points servant de vérité terrain. Nous générons des coordonnées autour de ces centres avec un tirage aléatoire gaussien. Si le point est en dehors de notre fenêtre de mesure [0,100]x[0,100], il n’est pas inséré dans la liste. Nous remplissons la liste nommée points avec des tuples contenant trois valeurs : x, y et l’identifiant de la catégorie.
Les dernières lignes permettent grâce à Matplotlib et à la fonction scatter() de représenter l’ensemble de ces points dans un graphique en utilisant la couleur associée à chaque catégorie :
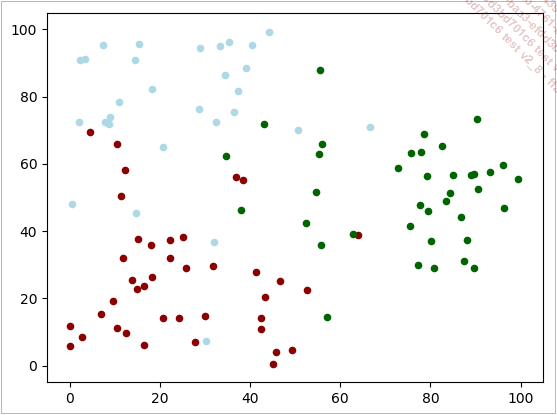
La question de la classification se pose maintenant simplement. On a nouvel échantillon de caractéristiques (20,20), quelle est sa catégorie ? Sur le graphique, ce point est entouré de points rouges, il est fort probable que sa catégorie soit rouge aussi. Si ses caractéristiques sont (40,60), il est entouré de deux points rouges et d’un point vert, on aurait tendance à dire qu’il appartient plutôt à la classe rouge.
Ainsi fonctionne l’algorithme des k plus proches voisins. Pour un point donné correspondant à un nouvel échantillon...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations


