Les boucles
Les structures itératives
1. Itérer pour mieux programmer
Dans le chapitre précédent, nous avons appris à guider notre algorithme en lui demandant de tester des conditions afin d’exécuter ou non des instructions. Ce fut le premier pas d’une réflexion importante pour communiquer quoi faire et surtout quand le faire à la machine. Passons maintenant au deuxième pas primordial : les itérations.
Reprenons les deux exemples du premier chapitre : la notice de montage d’un meuble en kit et la recette de la tarte aux pommes.
Dans le cas d’une notice de montage, il est souvent demandé de répéter les mêmes actions sur les mêmes types de pièces. Un exemple est représenté par la figure suivante : il nous est demandé d’insérer quatre vis dans une planche et de le faire pour les quatre planches. Il s’agit bien des mêmes actions à faire quatre fois, donc une itération de quatre tours. Le x4 de cette figure indique ce nombre d’itérations et nous semble parlant et tout à fait logique. Nous allons découvrir comment le traduire pour l’ordinateur dans la suite de ce chapitre.
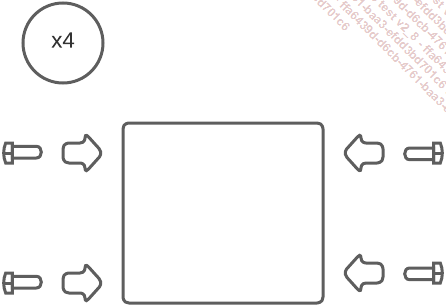
Une étape d’une notice de montage de meuble en kit
Pour la recette de cuisine, les répétitions se trouvent dans la gestion des pommes : pour chaque...
Tant Que
1. Principe et syntaxe
Nous pouvons comparer le TANT QUE à un SI ALORS qui se répète tant que la condition est valide. Cette structure réalise un nombre indéfini d’itérations qui va dépendre de la validité de la condition. Ces itérations ne s’arrêtent que lorsque la condition n’est plus validée.
Les instructions à répéter se retrouvent dans le bloc de cette structure :
TANT QUE (conditionnelle)
FAIRE
... // suite d'instructions à répéter
FINTANTQUE Revenons en cuisine avec notre tarte aux pommes. Une manière de gérer les pommes avec cette structure serait la suivante :
TANT QUE il reste des pommes
FAIRE
Prendre une pomme
Éplucher la pomme
Couper la pomme en tranches
FINTANTQUE La difficulté du TANT QUE est de trouver la bonne condition à tester. En effet, si cette condition est toujours satisfaite, votre itération sera infinie, elle se n’arrêtera jamais et votre programme restera bloqué sur les instructions du bloc, sans jamais se terminer. Si la condition n’est jamais satisfaite, la boucle ne s’exécute pas une seule fois. C’est ce que les développeurs appellent une boucle infinie.
Regardons maintenant...
Répéter ... Jusqu’à
1. Principe et syntaxe
Le REPETER JUSQU’A peut être considéré comme un TANT QUE inversé : les instructions sont d’abord répétées une fois avant de tester la condition. Quelle que soit la validité de la condition, les instructions du bloc sont forcément exécutées une fois.
REPETER
... // suite d'instructions à répéter
JUSQU'A (conditionnelle) Notre deuxième version pour la gestion des pommes de notre tarte est donc la suivante :
REPETER
FAIRE
Prendre une pomme
Éplucher la pomme
Couper la pomme en tranches
JUSQU'A il ne reste plus de pommes Nous pouvons remarquer que les conditions du TANT QUE et du REPETER JUSQU’A sont des conditions inverses. Nous testons s’il reste des pommes avec le TANTQUE alors que nous testons s’il ne reste plus de pommes avec le REPETER JUSQU’A.
2. Exemple
Corrigeons notre menu avec cette nouvelle structure itérative :
PROGRAMME Menu
VAR
reponse : CHAINE
DEBUT
REPETER
ECRIRE("Voulez-vous continuer? (oui/non)")
reponse <- LIRE() ...Pour
1. Principe et syntaxe
La structure itérative POUR correspond au cas de la répétition de la notice de montage du meuble en kit. Le bloc d’instruction est répété un nombre de fois précis, déterminé avant la structure.
Le POUR doit toujours être utilisé avec une variable qui nous permet de savoir à quel numéro d’itération nous sommes actuellement : le compteur, communément nommé i en programmation.
Ce compteur doit partir d’une valeur initiale pour arriver à une valeur finale. Lorsque ce dernier dépasse cette valeur finale, les itérations cessent et la suite du programme est exécutée.
Pour aller de la valeur initiale à la valeur finale, vous devez déclarer le pas : comment le compteur va changer de valeur d’une itération à l’autre. Ce pas est appliqué à chaque tour et doit être un entier, positif ou négatif. La valeur du pas est additionnée automatiquement au compteur à chaque nouvelle itération.
Si vous voulez écrire un POUR décroissant, qui décrémente donc le compteur, il vous suffit de déclarer un pas négatif.
VAR compteur : ENTIER
POUR compteur ALLANT de ... à ... AU PAS DE ...
FAIRE
... // suite...Structures itératives imbriquées
Nous avons un peu trop vulgarisé nos deux algorithmes de la vie courante. En effet, il y a un traitement à faire pour chaque tranche de pomme dans la recette, et un autre pour chaque vis dans la notice de montage. Nous avons donc besoin d’une itération dans une autre.
Comme pour la structure conditionnelle SI, vous pouvez tout à fait imbriquer des structures itératives les unes dans les autres et imbriquer des conditionnelles dans des itératives, et vice versa. Les possibilités d’imbrication sont infinies, ce qui nous permet d’écrire des programmes complexes intéressants pour l’utilisateur.
Détaillons maintenant nos deux exemples en imbriquant une structure itérative dans celles qui existent déjà :
PROGRAMME recette_tarte_pommes
TANT QUE il y a des pommes
FAIRE
Prendre une pomme
Eplucher la pomme
Couper la pomme en tranchess
REPETER
Disposer la tranche dans la tarte
JUSQU'A il ne reste plus de tranches
FINTANTQUE PROGRAMME Notice_complete
i, j : ENTIER
DEBUT
POUR i ALLANT de 1 à 4 AU PAS DE 1
FAIRE
POUR...Attention danger
Le premier danger des structures conditionnelles est la boucle infinie. Vous devez être certain que votre condition de sortie sera validée au cours de l’exécution de l’algorithme ou que votre compteur atteindra la borne maximale.
Prenons deux exemples de boucles infinies.
Le premier est un comptage avec la boucle TANT QUE :
PROGRAMME Comptage_infini
VAR
cpt : ENTIER <- 1
borne : ENTIER
DEBUT
ECRIRE("Entrez un nombre supérieur à 1")
borne <- LIRE()
TANT QUE cpt borne
FAIRE
ECRIRE(cpt)
FINTANTQUE
FIN Cet algorithme n’augmente jamais la valeur de la variable cpt. De ce fait, la valeur de cette variable sera toujours différente de celle de la variable borne et les itérations ne s’arrêteront jamais, 1 sera donc affiché à l’infini.
Si vous avez un nombre d’itérations fixes, utilisez toujours une structure POUR.
Le second est une légère modification de notre table de multiplication :
PROGRAMME Table_multiplication_infini
i : ENTIER
entree_utilisateur : ENTIER
DEBUT
ECRIRE("Quelle table voulez-vous afficher?") ...Itérons en python
1. Pour
L’une des particularités du langage Python est la structure POUR. En algorithmie, cette structure a besoin d’un compteur, d’une valeur initiale et d’une valeur finale de ce compteur et d’un pas. Python traduit cette structure par POUR CHAQUE.
Le POUR CHAQUE de Python itère sur un ensemble de valeurs et va mettre dans une variable chacune de ces valeurs, une par itération.
Sa syntaxe est la suivante :
for variable in ensemble_valeurs :
# bloc d'instructions à répéter Commençons par itérer sur une chaîne de caractères (qui est bien un ensemble de caractères) :.
for carac in "hello world" :
print(carac, end="")
print() # un saut de ligne en plus pour l'affichage Le for précédent affiche chaque caractère de la chaîne hello world sur une ligne, les uns après les autres.
Comment faire pour utiliser POUR CHAQUE afin d’écrire notre POUR ? Pour ce faire, il existe une instruction particulière en Python donnant un ensemble de valeurs numériques : le range.
Le range prend a minima en paramètre la borne maximale de l’ensemble. range(10) va nous donner les dix premiers entiers. Cette borne n’est pas comprise dans l’ensemble de valeurs retournées.
Par défaut, le range commence avec la valeur initiale 0. Si vous voulez commencer avec une autre valeur initiale, il faut l’indiquer en premier paramètre : range(1,11) retourne les 10 premiers entiers positifs.
Pour changer le pas qui est de 1 par défaut, il vous faut ajouter un troisième paramètre : range (1, 11, 2) donne les cinq premiers entiers impairs.
Utilisons donc...
Exercices
1. Exercice 1
Écrivez un algorithme qui affiche les vingt premiers termes de la table de multiplication en signalant les multiples de 3 avec un astérisque. Codez le script Python correspondant.
2. Exercice 2
Écrivez un algorithme qui calcule la multiplication de deux entiers entrés par l’utilisateur sans utiliser l’opérateur x (i.e. avec des additions successives). Codez le script Python correspondant.
3. Exercice 3
Écrivez un algorithme qui récupère plusieurs fois une chaîne de caractères entrée par l’utilisateur et en affiche sa longueur jusqu’à ce que cette entrée corresponde au mot "end". Codez le script Python correspondant.
4. Exercice 4
Écrivez un algorithme qui affiche les n premiers carrés, n étant un entier entré par l’utilisateur. Codez le script Python correspondant.
5. Exercice 5
Écrivez un algorithme qui implémente le jeu du FizzBuzz : afficher les cents premiers entiers en remplaçant les multiples de trois par Fizz, les multiples de cinq par Buzz et ceux de quinze par FizzBuzz. Codez le script Python correspondant en ajoutant que les sauts de ligne sont uniquement après les multiples de dix.
6. Exercice 6
Écrivez un algorithme qui détermine si une chaîne est un palindrome, c’est-à-dire un mot qui se lit aussi...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

