La trigonométrie
Introduction
La trigonométrie est utilisée dans de nombreux domaines de la recherche, de l’ingénierie et de la technique.
Les unités d’angles
Les arguments des fonctions trigonométriques d’Excel sont exprimés en radians (abréviation rd.). Les autres unités couramment utilisées en pratique sont :
-
Les degrés DMS (degrés, minutes, secondes.) : 43° 54’ 25.03", correspondant à la notation classique des cartographes.
-
Les degrés décimaux : 48,67489 plus simples à saisir sur un GPS.
-
Les grades, utilisées par les géomètres-topographes.
La mesure de la circonférence d’un cercle correspond à 2π radians soit 360° ou 400 grades. Le nombre π est obtenu dans Excel par la fonction PI().
Les deux figures suivantes résument les principales fonctions de conversion d’une unité à l’autre.
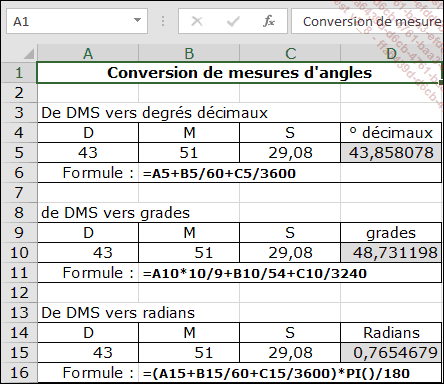
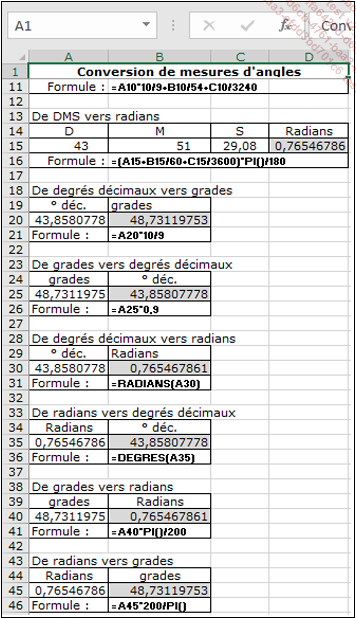
Les conversions vers les degrés DMS nécessitent la rédaction de fonctions personnalisées VBA (cf. chapitre Créer ses propres fonctions).
Les fonctions trigonométriques
Le tableau suivant récapitule les fonctions trigonométriques et les fonctions correspondantes d’Excel.
|
Fonction trigonométrique |
Fonction Excel |
|
Sin(x) |
=SIN(radians) |
|
Cos(x) |
=COS(radians) |
|
Tan(x) |
=TAN(radians) |
|
ArcSin(x) |
=ASIN(valeur) |
|
arcCos(x) |
=ACOS(valeur) |
|
arcTan(x) |
=ATAN(valeur) |
Ci-dessous, deux figures présentent les résultats de calculs trigonométriques classiques et les formules utilisées.
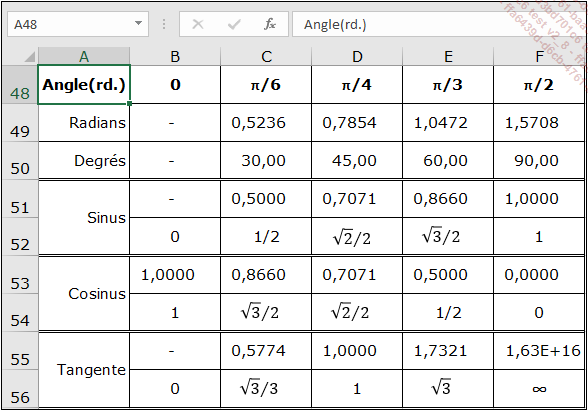
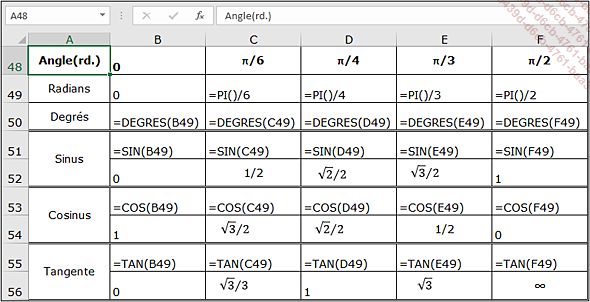
La résolution des triangles
La résolution des triangles est une technique utilisée dans les levés topographiques. Le triangle ci-dessous est utilisé dans les exemples qui suivent :
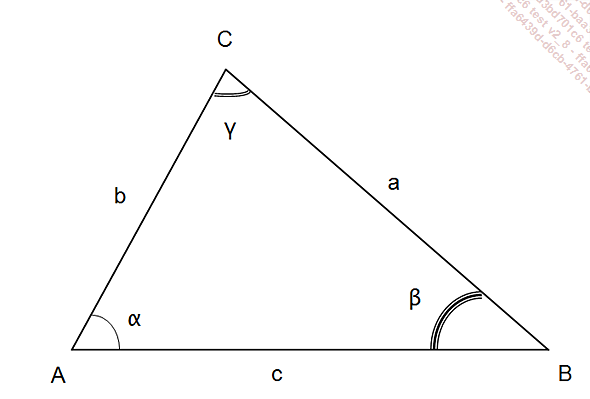
Calcul des angles (α,β,γ) de l’aire S connaissant les 3 côtés (a,b,c)
Les formules suivantes sont utilisées :
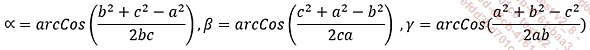
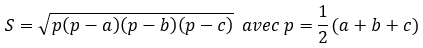
Les résultats seront calculés en degrés décimaux pour les angles, en m2 pour l’aire S et en mètres pour le demi-périmètre p.
Pour l’exemple, les dimensions suivantes : a=70 m, b=60 m et c=80 m sont utilisées.
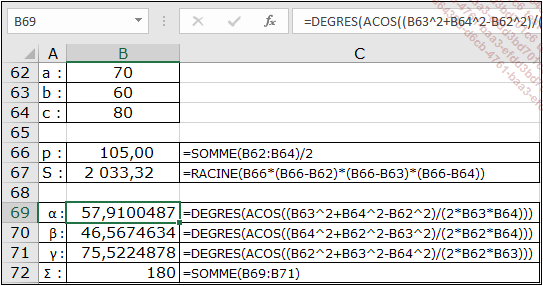
Le contenu de la cellule B72 permet de vérifier que la somme des angles du triangle est bien égale à 180°.
Calcul des angles α et β, de l’aire S et du côté c connaissant γ, a et b (un angle et les deux côtés adjacents connus)
Les formules sont les suivantes :
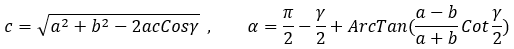
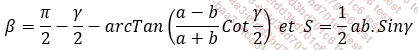
Dans les formules de l’extrait ci-dessous, les angles sont exprimés en degrés décimaux.
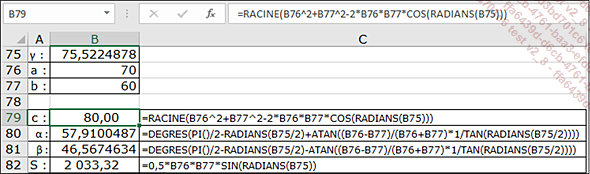
La valeur de l’angle γ, exprimée en degrés décimaux dans la cellule B75, doit bien entendu être transformée par la fonction RADIANS pour servir d’argument aux fonctions trigonométriques SIN, COS et TAN.
La cotangente est calculée comme l’inverse de la tangente.
Calcul des côtés a et b, de l’angle...
Application à la topographie
Calcul de la hauteur d’un point inaccessible
On veut calculer la dénivelée H d’un point inaccessible à partir de relevés angulaires α et β effectués sur une surface supposée plane. Le schéma est le suivant :
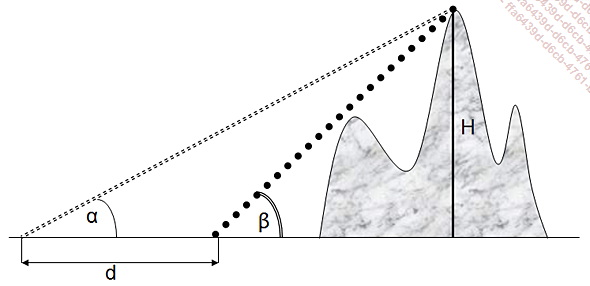
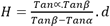
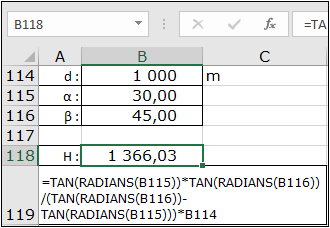
Ce qui donne dans Excel :
Arpentage (calcul de la surface d’un terrain)
Le terrain est assimilé à un polygone quelconque. L’arpenteur procède par découpage de la surface en triangles.
Dans le schéma suivant, l’arpenteur installe son théodolite au point T1 (il recommencera la manœuvre ensuite au point T2). Il implante des piquets aux différents sommets du polygone (A, B, C, D, E, F, G). Il mesure ensuite, à la chaîne d’arpenteur, les distances (a, b, g, f, h) et (c, d, e, j). La mesure de j n’est pas indispensable. Depuis le point T1 il mesure les angles BT1A, AT1G, etc.
Le calcul de la surface de chaque triangle est obtenu par la formule :
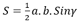 et la longueur
du côté opposé par :
et la longueur
du côté opposé par : 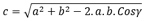 dans lesquelles a et b sont les longueurs des
côtés d’un angle γ et
c la longueur du côté opposé. Grâce à ces
formules, la surface et le périmètre du terrain
peuvent être calculés.
dans lesquelles a et b sont les longueurs des
côtés d’un angle γ et
c la longueur du côté opposé. Grâce à ces
formules, la surface et le périmètre du terrain
peuvent être calculés.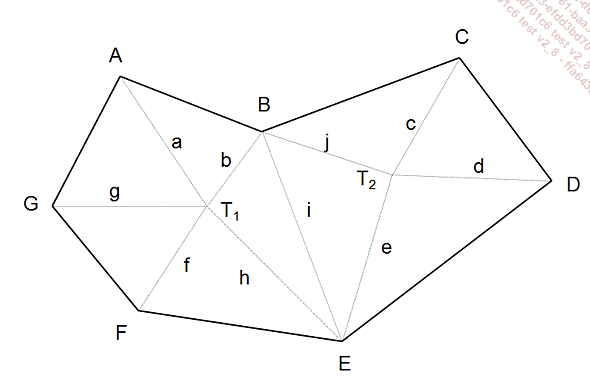
L’exemple ci-après présente le calcul de la surface...
Astronomie : détermination de la position d’une étoile
Le problème de la détermination de la position d’une étoile sur la sphère céleste à partir de la position de l’observateur est tributaire de la rotation de la Terre. En effet, la position de l’étoile est fixe (tout au moins à l’échelle d’une durée de vie humaine) alors que celle de l’observateur est variable.
Le repère d’observation est constitué de la façon suivante (cf. schéma suivant) :
-
L’observateur se trouve au point O, à la surface de la Terre. Le point E correspond au méridien du lieu d’observation (la direction Nord-sud).
-
L’étoile observée se trouve en M sur la sphère céleste.
-
L’équateur céleste est l’intersection du plan tangent à la Terre en O avec la sphère céleste.
-
Le point γ est le point vernal, origine des longitudes célestes.
-
L’angle H est l’angle horaire de l’étoile.
-
L’angle T (variable) est l’angle horaire du point γ. Il s’appelle aussi "temps sidéral local" mais c’est bien un angle !
-
L’angle α (fixe) est l’ascension droite de l’étoile.
-
L’angle δ (fixe) est la déclinaison de l’étoile.
En résumé...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
