Les calculs financiers
Les remboursements de prêts
Les remboursements de prêts mettent en jeu le montant prêté, la durée de remboursement, le taux d’intérêt appliqué et les modalités de remboursement (terme échu ou à échoir). La notion de taux d’intérêt nécessite d’être précisée puisqu’elle représente le prix de l’argent.
Le taux d’intérêt de période
Les taux d’intérêt sont en général fournis en se ramenant à une période annuelle. Dans la pratique, les flux d’argent peuvent bien entendu avoir des périodicités quelconques : mois, trimestre ou semestre par exemple. Ces périodicités ne sont pas neutres.
Prenons un exemple simple : un créancier prête à un emprunteur, au taux annuel nominal de 2,4 % une somme de 10.000 € que ce dernier s’engage à lui rembourser un an plus tard.
1er cas : l’emprunteur rembourse au bout d’un an la somme de 10.240 € (10.000 + 240 € d’intérêts). Dans ce cas, le taux de la période est identique au taux nominal, soit 2,4 %.
2e cas : par prudence, le prêteur demande un premier remboursement de 5.120 € au bout de 6 mois et les 5.120 € restants au bout d’un an. On peut donc considérer que l’emprunteur subit un coût supplémentaire du fait par exemple qu’il va emprunter auprès d’un autre prêteur ces 5.120 € à un taux supposé identique de 2,4 %. Les intérêts pour ce 2e emprunt seront de : 5.120 x 2,4 % x 6/12 = 61,44 €. Au final, l’emprunteur aura payé 240+61,44=301,44 € d’intérêt, autrement dit le taux effectif de l’emprunt sera...
Les calculs d’actualisation
La valeur nette actualisée (flux périodiques)
La valeur nette actualisée est un outil servant à déterminer la rentabilité d’un investissement. Un investissement I effectué au temps n=0 va générer des flux de trésoreries CFi aux temps n=1, n=2,..., n=p. Ces flux de trésorerie sont pondérés par un taux d’actualisation ta et par le n° de la période correspondant au flux.
La formule de la valeur nette actualisée est la suivante :
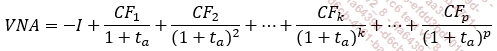
La fonction Excel VAN calcule le montant global des valeurs actualisées des flux de trésorerie. Pour obtenir la Valeur Nette Actualisée, il faut donc enlever le montant de l’investissement initial. La syntaxe de la fonction est :
=VAN(taux d’actualisation;plage des flux)
L’exemple ci-dessous présente une application de la fonction VAN.
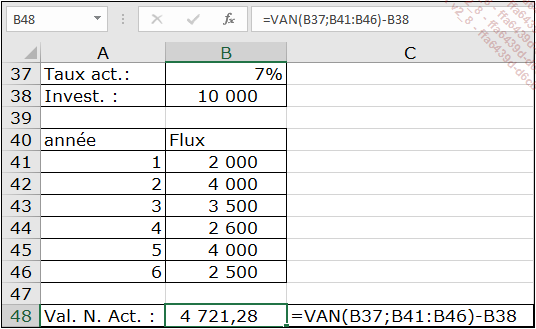
Ce calcul permet de conclure que la valeur nette actualisée des flux, diminuée de la valeur de l’investissement étant positive (4.721,28), l’investissement est considéré comme rentable.
Le taux de rentablilité interne (flux périodiques)
Le taux de rentabilité interne d’un investissement est le taux correspondant à une Valeur Nette Actualisée égale à 0. Ce taux est calculable dans Excel par la fonction TRI dont...
Les calculs d’amortissement
L’amortissement linéaire
L’amortissement linéaire consiste à affecter une dotation aux amortissements proportionnelle au temps. C’est un calcul relativement simple, pour lequel la fonction AMORLIN proposée par Excel n’est d’aucune utilité.
Exemple
Une immobilisation d’une valeur de 10.000 € est acquise le 1er juillet 2019. La durée d’amortissement est de 5 ans, soit 20 % de la valeur sur un exercice complet. Les dotations aux amortissements seront donc les suivantes :
-
2019 : 10.000 x 20 % x 0,5 = 1.000 (approximativement)
-
2020 : 2.000
-
2021 : 2.000
-
2022 : 2.000
-
2023 : 2.000
-
2024 : 1.000 (le solde)
Le tableau Excel suivant traite l’amortissement linéaire quelle que soit la durée d’amortissement. Pour le 1er exercice, la durée d’amortissement est calculée au jour près.
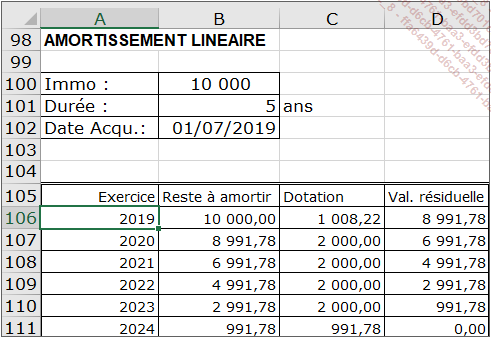
Au-delà du 2e exercice, les lignes de calculs peuvent être reproduites par simple copie pour atteindre le maximum de durée d’amortissement prévue.
Les formules utilisées sont les suivantes :
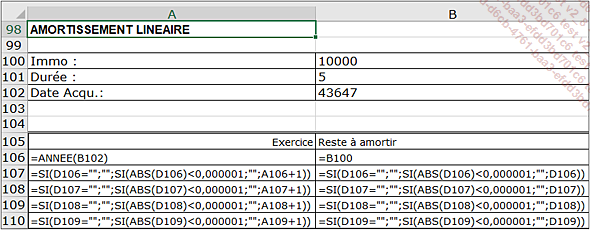
En A106 et B106, les formules sont évidentes.
La formule de la colonne Exercice (A), à partir de A107, est la suivante :
=SI(D106="";"";SI(ABS(D106)<0,000001;"";A106+1))
Elle permet d’exprimer la logique suivante : si la valeur résiduelle de l’exercice précédent (D106) est vide, alors l’exercice est vide, sinon, si cette même valeur résiduelle est quasiment égale à 0 alors l’exercice est vide et sinon...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations
