Présentation du chapitre

De nombreux domaines font face à un problème de recherche de chemins, appelé "pathfinding" en anglais. On pense tout d’abord aux GPS et aux logiciels de recherche d’itinéraires (en voiture, en train, en transport en commun...), voire aux jeux vidéo dans lesquels les ennemis doivent arriver sur le joueur par le chemin le plus court.

La recherche de chemins est en réalité un domaine bien plus vaste. En effet, de nombreux problèmes peuvent être représentés sous la forme d’un graphe, comme l’enchaînement des mouvements dans un jeu d’échecs.

La recherche d’un chemin dans ce cas-là peut être vue comme la recherche de la suite des mouvements à faire pour gagner.

Ce chapitre commence par présenter les différents concepts de théorie des graphes, et les définitions associées. Les algorithmes fondamentaux sont ensuite présentés, avec leur fonctionnement et leurs contraintes.

Les principaux domaines dans lesquels on peut utiliser cette recherche de chemins sont alors indiqués et un exemple d’implémentation des algorithmes en Java est présenté et appliqué à une recherche de chemins dans un environnement en 2D.

Le chapitre se termine par une synthèse.

Chemins et graphes

Un chemin peut être vu comme un parcours dans un graphe. Les principaux algorithmes se basent donc sur la théorie des graphes.

1. Définition et concepts

Un graphe est un ensemble de nœuds ou sommets (qui peuvent représenter par exemple des villes) liés par des arcs, qui seraient alors des routes.

Voici un graphe qui représente des gares et les liens qui existent entre ces gares (en train, sans changement) :

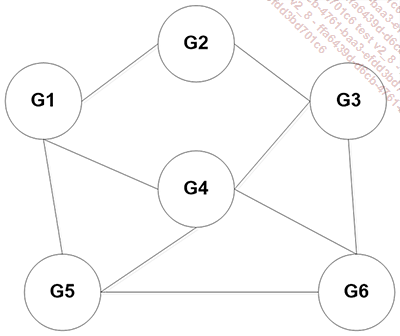
Les gares de G1 à G6 sont donc les nœuds. L’arc allant de G5 à G6 indique la présence d’un lien direct entre ces deux gares. Il est noté (G5, G6) ou (G6, G5) selon le sens voulu.

Par contre pour aller de G1 à G6, il n’y a pas de lien direct, il faudra passer par G4 ou G5 si on ne souhaite qu’un changement, ou par G2 puis G3 avec deux changements.

Un chemin permet de rejoindre différents sommets liés entre eux par des arcs. Ainsi, G1-G2-G3-G6 est un chemin de longueur 3 (la longueur est le nombre d’arcs suivis).

On parle de circuit lorsqu’on peut partir d’un nœud et y revenir. Ici, le graphe contient de nombreux circuits, comme G1-G4-G5-G1 ou G4-G5-G6-G4.

L’ordre d’un graphe correspond au nombre de sommets qu’il contient. Notre exemple contient 6 gares, il s’agit donc d’un graphe d’ordre 6.

Deux nœuds sont dits adjacents (ou voisins) s’il existe un lien permettant...

Exemple en cartographie

Pour étudier les différents algorithmes, nous allons nous intéresser à un petit jeu dans lequel nous contrôlons un personnage qui est un explorateur. Comme dans beaucoup de jeux de rôle, notre héros est limité à chaque tour (il n’a le droit qu’à un certain nombre de points d’action). Pour aller le plus vite d’un point à un autre, nous cherchons le chemin le plus court sur la carte, en prenant en compte les types de terrains.

Il en existe de plusieurs sortes, requérant plus ou moins d’énergie (et donc de points d’action) :

Des chemins, qui nécessitent un point d’action par case.
De l’herbe, nécessitant deux points d’action.
Des ponts, nécessitant deux points d’action.
De l’eau, infranchissable.
Et des arbres, infranchissables aussi.

La carte est la suivante :

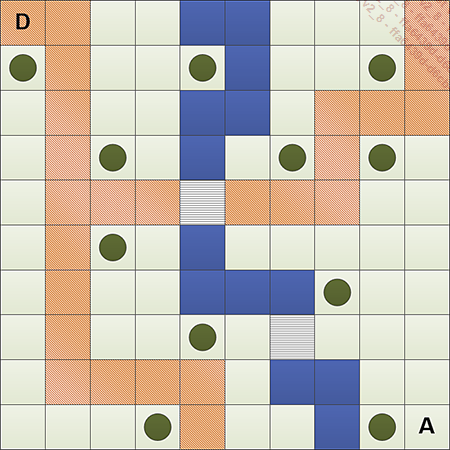
Et la légende :

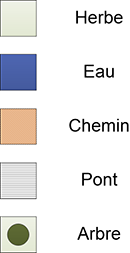
Nous cherchons donc le chemin permettant de relier le départ (D) à l’arrivée (A), et ce en utilisant le moins de points d’action possible. Le chemin le plus court coûte 27 points d’action (en suivant le chemin et en passant le premier pont, puis en coupant par l’herbe à la fin).

Algorithmes naïfs de recherche de chemins

Ces premiers algorithmes ne sont pas "intelligents" : ils sont dits naïfs, car ils n’utilisent pas de connaissances sur le problème pour agir. Dans le pire des cas, ils testent tous les chemins possibles pour déterminer s’il existe bien un chemin entre deux nœuds.

De plus, rien n’indique que le chemin trouvé est bien le plus court. Ils sont cependant faciles à implémenter.

1. Parcours en profondeur

C’est l’algorithme que l’on essaie naturellement dans un labyrinthe : on cherche à avancer le plus possible, et, si on est coincé, on revient à la dernière intersection que l’on a rencontrée et on teste un nouveau chemin.

Cet algorithme ne permet pas de déterminer le chemin le plus court, mais simplement de trouver un chemin.

a. Principe et pseudo-code

Son fonctionnement est assez simple.

Tout d’abord, on choisit l’ordre des parcours des nœuds puis on applique cet ordre pour avancer un maximum. Si l’on est bloqué, on retourne en arrière, et on teste la deuxième possibilité.

Le parcours en profondeur permet donc de déterminer l’existence d’un chemin, mais il ne prend pas en compte les longueurs des arcs, et donc ne permet pas de dire si l’on a trouvé le chemin le plus court.

De plus, le résultat obtenu dépend fortement de l’ordre choisi pour le parcours du graphe, l’ordre optimal dépendant du problème et ne pouvant être déterminé a priori. Bien souvent, il n’est donc pas efficace. Dans le pire des cas, il doit même tester toutes les possibilités pour trouver un chemin.

Il est cependant facile à implémenter. En effet, nous allons conserver une liste des nœuds visités. À chaque fois que l’on se trouve sur un nœud, nous allons ajouter tous ses voisins non visités à une pile dans l’ordre choisi. Ensuite, nous dépilons le premier élément de celui-ci.

Une pile (ou LIFO pour Last In, First Out) est une structure algorithmique dans laquelle les éléments sont ajoutés en haut, et enlevés en partant du haut, comme une pile de vêtements, de papiers... Il n’est pas possible d’enlever...

Algorithmes "intelligents"

Les parcours en profondeur et en largeur ne permettent pas de trouver le chemin le plus court, mais juste le premier qui permet de joindre le point de départ au point d’arrivée.

D’autres algorithmes existent, qui permettent de déterminer le chemin le plus court, ou au moins un chemin optimisé, et ce sans forcément avoir à tester tous les chemins possibles.

1. Algorithme de Bellman-Ford

L’algorithme de Bellman-Ford permet de trouver le chemin le plus court s’il existe. Il n’est pas le plus optimisé, mais c’est celui qui fonctionne dans le plus de cas. En effet, il accepte des longueurs négatives pour les arcs, et pas seulement des positives.

De plus, s’il y a un circuit dont la longueur est négative (et donc qui permet de diminuer le poids total), il peut le détecter. C’est important, car dans ce cas-là il n’existe pas de chemin le plus court.

a. Principe et pseudo-code

Cet algorithme va utiliser la matrice des longueurs. Son fonctionnement est itératif.

Au départ, on initialise à +∞ la longueur minimale de chaque nœud (ce qui signifie que l’on n’a pas encore trouvé de chemin jusque-là depuis l’arrivée). On va aussi garder pour chaque nœud le nœud précédent (celui qui permet d’y arriver avec la plus faible longueur) et l’initialiser au nœud vide.

On applique ensuite autant de fois que le nombre de nœuds moins 1 la même boucle. Ainsi, s’il y a 7 nœuds, on l’applique 6 fois.

À chaque itération, on suit chaque arc (u,v). On calcule la distance depuis le point de départ à v comme étant la distance du départ à u, plus la longueur de l’arc (u,v). On obtient ainsi une nouvelle longueur pour aller au nœud v que l’on compare à celle déjà enregistrée. Si cette longueur est plus faible que celle obtenue jusqu’ici, alors on change la longueur de ce nœud et on indique que son prédécesseur est maintenant u.

Seuls les arcs partant d’un nœud dont la distance calculée est différente de +∞ ont besoin d’être utilisés. En effet, dans le cas contraire on garde une distance infinie...

Domaines d’application

Ces algorithmes de recherche de chemins sont utilisés dans de nombreux domaines.

Le premier domaine est celui de la recherche d’itinéraires. Tous les GPS et les applications permettant d’aller d’un endroit à l’autre (en train, en bus, en métro, à pied...) utilisent des algorithmes de pathfinding. Ils prennent en compte la longueur du chemin ou son temps. Vue la complexité des cartes souvent utilisées (par exemple pour Google Maps), il est évident que les algorithmes doivent être optimisés, et privilégient les grands axes dès que possible. Le détail des algorithmes n’est bien évidemment pas communiqué.

Cette recherche de chemins se retrouve dans les jeux vidéo. Le but est alors de déplacer un personnage (contrôlé par le joueur ou représentant un ennemi) d’un endroit à un autre. Les cartes peuvent être très grandes, et le nombre de personnages important. Là encore, il faut optimiser les algorithmes utilisés. On peut cependant noter que c’est l’algorithme A* qui est majoritairement implémenté.

La robotique est un autre domaine friand de recherche d’itinéraires. Il s’agit alors d’amener un robot d’un point à un autre, le plus rapidement possible. Ces algorithmes sont généralement...

Implémentation

Nous allons passer à l’implémentation de ces algorithmes. Le code sera cependant très générique, ce qui permettra d’ajouter facilement de nouvelles méthodes de résolution ou de nouveaux problèmes à résoudre.

Nous l’appliquerons au problème de la carte ensuite, à travers une application console.

1. Nœuds, arcs et graphes

La première étape est la définition de nos graphes. Nous allons commencer par les nœuds, puis nous verrons les arcs qui les relient et enfin le graphe complet.

a. Implémentation des nœuds

Les nœuds sont les structures de base de nos graphes. Cependant, le contenu réel d’un nœud dépend fortement du problème à résoudre : il peut s’agir de gares, de cases sur une grille, de serveurs, de villes...

Nous créons donc une classe abstraite Noeud, qui contiendra les informations nécessaires pour les algorithmes. Cette classe doit être héritée pour la résolution pratique d’un problème.

Les nœuds ont besoin de trois informations :

Le précurseur, qui est aussi un nœud.
La distance depuis le départ.
La distance estimée à la sortie (si nécessaire).

Nous utilisons des attributs publics pour simplifier les accès (cela évite les accesseurs/mutateurs). Pour les deux premiers, nous avons des valeurs par défaut.

public abstract class Noeud {  
   public Noeud precurseur = null;  
   public double distanceDuDepart = Double.POSITIVE_INFINITY; 
   public double distanceEstimee;     
}

b. Classe représentant les arcs

Une fois les nœuds définis, nous pouvons définir les arcs, grâce à la classe Arc. Ceux-ci contiennent trois propriétés :

Le nœud de départ de l’arc.
Le nœud d’arrivée.
La longueur ou coût de l’arc.

Un constructeur est ajouté pour initialiser plus rapidement les trois propriétés :

public class Arc {  
   protected Noeud source;  
   protected Noeud cible;  
   protected double cout;  
     
   public Arc(Noeud _source, Noeud _cible...

Synthèse

La recherche de chemins, ou pathfinding, permet de relier des nœuds d’un graphe en utilisant des arcs prédéfinis. Ceux-ci sont associés à une longueur (ou coût). On peut ainsi chercher le chemin au coût le plus faible, que le coût soit en réalité un kilométrage, un temps ou encore un prix (par exemple l’essence consommée).

Plusieurs algorithmes existent, chacun ayant ses spécificités.

Lorsque l’on cherche principalement à savoir si un chemin existe, sans rechercher le plus court, on peut se tourner vers les algorithmes naïfs de recherche en profondeur ou en largeur. Si on sait globalement dans quelle direction aller, la recherche en profondeur peut être intéressante (à condition de bien préciser l’ordre de parcours des voisins).

La recherche en largeur donne généralement de meilleurs résultats et est surtout plus générique. Dans les deux cas, on avance de nœud en nœud et on mémorise les nouveaux nœuds adjacents découverts, que l’on visitera ultérieurement. Ce qui les différencie, c’est la structure utilisée pour stocker les voisins : une pile pour la recherche en profondeur et une file pour la recherche en largeur.

L’algorithme de Bellman-Ford permet, quant à lui, de trouver le chemin...