Les statistiques
Notions clés sur les statistiques
1. Histoire rapide de la discipline des statistiques
Le terme "statistique" daterait de 1746, mais les statistiques existent depuis le début de la civilisation humaine. Les premières statistiques s’intéressent principalement à la collecte de données d’état, c’est-à-dire à la mesure et à l’enregistrement de valeurs. En effet, les cordes à nœuds ou le comptage à encoches ont posé les bases des statistiques en permettant de récolter, de conserver et de comparer les états d’une population humaine (nombre de naissances, de morts, mais aussi métiers, mariages/alliances…), animale (nombre d’individus, production laitière…) ou végétale (date de récolte, rendement agricole…) ou de son environnement (cartographie...).
Depuis le XVIIIe siècle, avec le développement de la théorie des probabilités en mathématiques, la discipline a évolué pour intégrer, en plus de la récolte, l’analyse puis la valorisation des données.
La théorie des probabilités est en mathématiques l’étude des événements marquée par l’incertitude et le hasard. Tout le monde conçoit qu’une pièce équilibrée a la même "chance" de tomber du côté pile que du côté face, sans pouvoir prédire de quel côté elle va réellement tomber. Les lois de probabilités statistiques permettent de modéliser, de calculer, de prédire les événements aléatoires.
Initialement réservées au recensement d’états, les statistiques accompagnent maintenant des domaines variés...
Initiation à la réalisation de graphiques avec {ggplot2} dans R
Il existe plusieurs fonctions et packages qui permettent de faire des graphiques dans R, {ggplot2} est celui compris dans {tidyverse}. D’autres sont abordés dans la suite de l’ouvrage, même s’ils restent minoritaires.
La construction de graphiques avec {ggplot2} se fait par couches, c’est-à-dire que l’ordre des commandes influence la superposition des éléments du graphique. Les différents éléments s’ajoutent ensemble grâce au signe +.
Pour commencer, il faut donner le nom du jeu de données représenté par le graphique. Par exemple, iris est un jeu de données présent dans le package {datasets} chargé automatiquement dans R, qui donne les mesures en centimètres des longueurs et largeurs des pétales et sépales de 50 fleurs de 3 espèces d’iris.
Ensuite, il faut déterminer les variables d’intérêt avec la fonction aes() du package {ggplot2} : généralement, la variable à mettre en abscisses, x, sera la variable explicative, et la variable à mettre en ordonnées, y, sera la variable à expliquer. Par exemple, la largeur des pétales expliquée par leur longueur s’écrit :
ggplot(
data = iris,
mapping =
aes(
x = Petal.Length,
y = Petal.Width
)
) Ce code donne un graphique vide, car aucun type de représentation n’a été sélectionné :
Figure 02-01 : Graphique vide des largeurs des pétales d’iris expliquées par leurs longueurs. ...
Lois de probabilités statistiques
1. Introduction aux lois de probabilités
Les lois de probabilités sont des outils pour pouvoir généraliser les données. Elles s’appuient sur des paramètres qui définissent les lois de probabilités. Les tests statistiques qui utilisent les lois de probabilités sont dits paramétriques.
Une loi de probabilités revient à prévoir le comportement d’une expérience aléatoire. Les grandes lois de probabilités sont basées sur le fonctionnement de jeux de hasard et ont été ensuite formalisées. Naturellement, tout le monde comprend que lorsqu’on joue à lancer une pièce (équilibrée) au hasard, chacune des faces à autant de chance de sortir. Il est impossible de prévoir le nombre de piles et de faces pour un petit nombre de lancers, par exemple six. Par contre, plus ce nombre augmente, plus on peut prévoir le nombre de fois que le côté face va sortir, car le nombre de lancers équilibre le résultat :
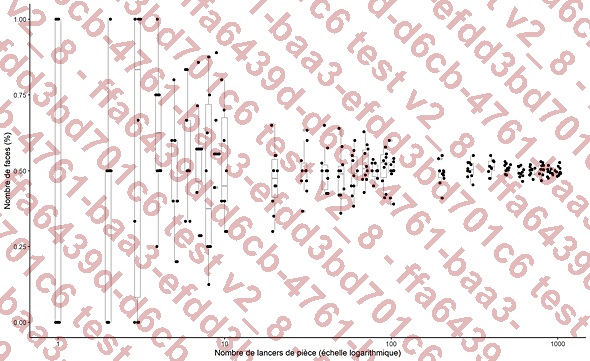
Figure 02-06 : Pourcentage de succès (obtenir le côté face) lorsque le nombre de lancers est augmenté. Plus il y a de lancers, plus le pourcentage de succès s’approche de l’attendu (50 %). L’expérience a été modélisée 10 fois par nombre de lancers (points noirs). Visibles en arrière-plan, les boxplots (boîtes à moustaches) sont des éléments graphiques importants à utiliser (cf. section Réalisation de statistiques descriptives dans R).
# création d'un vecteur contenant le nombre de lancers
nb_lancers <- c(
1:9, # 1, 2, 3... 9
seq(from = 10, to = 100, by = 10), # 10, 20... 100
seq(from = 200...Réalisation de statistiques descriptives dans R
1. Principe des statistiques descriptives
Comme son nom l’indique, le but des statistiques descriptives est de décrire, donc de qualifier, de quantifier, de résumer et de représenter des données récoltées.
Au contraire des statistiques inférentielles, qui cherchent à élargir à la population les observations réalisées, ou aux statistiques prédictives, qui cherchent à modéliser les changements à venir, les statistiques descriptives se limitent aux données récoltées sur un échantillon donné et un pas de temps fixé. C’est une première étape indispensable avant de généraliser, de prédire ou de modéliser.
Basées sur des calculs et des graphiques simples, les statistiques descriptives donnent un aperçu des données. Elles utilisent les lois de probabilités pour caractériser les données récoltées, détecter une tendance et même définir des valeurs extrêmes (outliers).
La description des données passe par le calcul de certains indicateurs comme la moyenne, l’écart-type, les extremums…
Face à un nouveau jeu de données, il faut commencer par traiter les variables séparément : ce sont les statistiques descriptives univariées ; puis, deux à deux : ce sont les statistiques descriptives bivariées.
2. Statistiques descriptives univariées dans R
a. Type de données
L’idée est d’en apprendre plus sur les données, variable par variable.
La première question à se poser est le type de variable : qualitative ou quantitative. Si la variable est qualitative, il faut regarder le type et le nombre...
Détection et visualisation des données manquantes dans R
Avant de voir comment détecter et traiter les données manquantes, il faut commencer par penser à ce que cela signifie. En effet, certaines fois, les données manquantes sont réellement absentes du tableau de données, et dans ce cas, la case vide permet de voir qu’il manque une information. D’autres fois, elles sont masquées, car remplacées par des valeurs généralistes, comme 0, NA, NULL, ou plus spécifiques et dépendantes du jeu de données, comme 99999, vide, non mesurée, Z…
Dans tous les cas, il faut être capable de les identifier, de les quantifier et de les traiter, en gardant en tête ce qu’elles signifient : manque d’une mesure, disparition d’un individu de l’échantillon, suppression involontaire…
L’étape d’identification se fait généralement au moment de l’analyse descriptive univariée. Une modalité sous ou sur-représentée est à regarder avec intérêt, comme le nom ou le sens des modalités.
Une fois identifiées, les données manquantes peuvent être quantifiées pour chaque variable et sur le jeu de données. Des fonctions aident dans ce cas, comme la fonction summary(), qui génère un tableau résumé du jeu de données, ou la fonction gg_miss_var() du package {naniar} qui montre graphiquement par défaut le nombre (show_pct...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations