Les tests d'hypothèses
Vocabulaire lié aux tests d’hypothèses
En statistiques, les réponses ne sont jamais tranchées. Il y a toujours une part d’aléatoire, d’imprévu, d’écart. C’est normal car sans cette part, les statistiques ne seraient pas nécessaires. Si un événement est certain, il n’y a pas besoin de loi de probabilités ou de test pour le prédire.
En statistiques, les tests, ou plus précisément les tests d’hypothèses, sont un outil, une règle de décision, qui permet de rejeter ou non une hypothèse, une réponse avec un risque connu. Le risque zéro dans l’absolu n’existe que dans les domaines où les statistiques ne sont pas nécessaires.
 . Rejeter
. Rejeter  revient à accepter l’hypothèse alternative
revient à accepter l’hypothèse alternative  : les données ne suivent pas
une loi normale.
: les données ne suivent pas
une loi normale. est rejetée alors qu’elle
est vraie. La probabilité associée à cette
erreur est le seuil de significativité,
est rejetée alors qu’elle
est vraie. La probabilité associée à cette
erreur est le seuil de significativité,  , généralement fixé à 5 %,
soit
, généralement fixé à 5 %,
soit  . L’erreur...
. L’erreur...Démarche du test d’hypothèses
La démarche du test d’hypothèses est toujours la même, quel que soit le test d’hypothèses réalisé :
-
1re étape : Définir les hypothèses.
Cas de l’autotest COVID : l’autotest permet de déterminer la présence de COVID ou l’autotest permet de déterminer l’absence de COVID. Afin de minimiser l’erreur de première espèce en suivant les attendus de la Haute Autorité de santé, l’autotest permet de déterminer l’absence de COVID.
-
2e étape : Formaliser les hypothèses.
Cas de l’autotest COVID :
= La COVID n’est pas présente dans l’échantillon.
= La COVID est présente dans l’échantillon.
-
3e étape : Définir le seuil de significativité (
) et la puissance minimale acceptée (
). Il faut aussi définir le type de test : bilatéral, unilatéral à droite ou à gauche. Le type de test est aussi dépendant de la statistique de test choisie.
Cas de l’autotest COVID :
= 0,99, donc
= 0,001.
= 0,080, la puissance minimale acceptée.
-
4e étape : Calculer la statistique de test et la probabilité que
soit vraie en fonction des données et des hypothèses définies pour savoir si l’hypothèse nulle est rejetée et/ou calculer la sensibilité et la spécificité pour valider le test réalisé.
Cas de l’autotest COVID : la sensibilité du test clinique est égale à 0,979 alors que la spécificité est égale à 0,995.
-
5e étape : Conclure en comparant la statistique de test et la valeur critique ou la probabilité calculée...
Test de Shapiro-Wilk
Le test de Shapiro-Wilk permet de vérifier qu’une variable suit une loi normale.
Initialement, le test de Shapiro ne pouvait s’appliquer que sur des variables ayant entre 3 et 50 observations. Suite à plusieurs développements, le nombre maximal d’observations a été repoussé pour atteindre la limite actuelle de 5 000.
shapiro.test(rnorm(10000, mean = 5, sd = 3))
# Error in shapiro.test(rnorm(10000, mean = 5, sd = 3)) :
sample size must be between 3 and 5000 Ce test ne se base sur aucune loi de probabilités, c’est donc bien un test non paramétrique.
 avec :
avec :-
X, la variable continue ordonnée de manière croissante ;
-
, la taille de X ;
-
, la moyenne de l’échantillon ;
-
, la partie entière de m ;
-
, le coefficient de pondération associé à l’individu i. Les coefficients de pondération sont disponibles dans une table non fournie ici.
 . Ce test
est unilatéral à gauche. Donc, si
. Ce test
est unilatéral à gauche. Donc, si  ,
,  est rejetée
et il est possible de conclure que la variable ne suit pas une loi
normale. Les valeurs seuil sont fournies par la table de
Shapiro-Wilk. Généralement, c’est la
est rejetée
et il est possible de conclure que la variable ne suit pas une loi
normale. Les valeurs seuil sont fournies par la table de
Shapiro-Wilk. Généralement, c’est la  du test qui est considérée.
Si la p-value est inférieure au seuil de significativité, c’est-à-dire
si
du test qui est considérée.
Si la p-value est inférieure au seuil de significativité, c’est-à-dire
si  , alors
, alors  est rejetée et les données
ne suivent pas une loi normale.
est rejetée et les données
ne suivent pas une loi normale.Le test de Shapiro-Wilk est très simple à réaliser dans R.
shapiro.test(iris$Petal.Length) 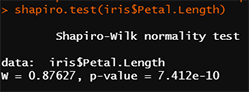
Figure 04-02 : La sortie du test de Shapiro-Wilk montre que la longueur des pétales du jeu de données iris ne suit pas une loi normale.
Le QQplot est souvent le graphique utilisé pour vérifier qu’une variable suit...
Test du Khi-2
1. Paramétrique ou non paramétrique, le test du Khi-2 ?
Le test du Khi-2 (ou Khi-deux ou X2) se réalise sur un tableau de comptage et est considéré comme non paramétrique par les mathématiciens et paramétrique par les biologistes. En fait, le nom "test du Khi-2" englobe différents tests qui utilisent tous la loi de probabilités du Khi-2, mais qui n’ont ni le même objectif ni la même utilisation :
-
Le test du Khi-2 d’adéquation ou de conformité vérifie que les observations d’un échantillon sont comparables à celles d’une loi de probabilités choisie. Ce test est paramétrique, car il demande de sélectionner une loi de probabilités (normale…).
-
Le test du Khi-2 d’indépendance mesure l’absence de relation entre deux variables dans un tableau de comptage. Ce test est non paramétrique, car il n’attend pas de loi de probabilités.
-
Le test du Khi-2 d’homogénéité vérifie que les observations sont similaires d’un pas de temps (intervalle de temps entre deux observations successives) à l’autre. Ce test est considéré comme non paramétrique même s’il s’appuie sur une distribution homogène entre les modalités donc sur la loi de probabilités uniforme.

Pour que le test du Khi-2 soit valide, il faut que la plus petite valeur attendue soit égale...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations