Réseaux de neurones à convolution
Objectifs du chapitre et prérequis
Dans le chapitre précédent, nous avons introduit les réseaux de neurones profonds. Nous avons vu que ces réseaux sont simplement constitués d’un empilement d’opérations simples, regroupées en couches, et appliquées successivement à un certain nombre de variables d’entrée.
Ce chapitre introduit un type de réseau de neurones particulier, le réseau de neurones à convolution, spécialement adapté pour traiter des images. Comme les réseaux de neurones profonds, les réseaux de neurones à convolution sont constitués d’un empilement de couches. Ces couches regroupent des opérations d’un type spécifiquement adapté au traitement d’images.
Nous verrons tout d’abord la motivation qui a conduit à l’invention de ces réseaux, leur historique, et leurs applications dans plusieurs contextes.
Les réseaux pour la classification sont ceux dont l’architecture est la plus simple. Dans ce chapitre, nous décrirons donc uniquement les réseaux utilisés pour la classification ; nous verrons dans les chapitres Détection, Segmentation et Applications spécifiques qu’ils peuvent être facilement étendus à d’autres applications.
Nous décrirons tout d’abord...
Motivation, historique et applications des réseaux de neurones à convolution
1. Motivation
Imaginons que nous souhaitions appliquer un réseau de neurones conventionnel à une image.
Pour les besoins de la démonstration, imaginons que cette image soit de taille très réduite, soit 32 x 32 pixels (ce qui est suffisant pour classifier des caractères, par exemple, mais pas pour distinguer un animal d’un autre), et que notre réseau de neurones ne comporte qu’une seule couche cachée.
La première étape consiste à aplatir l’image d’entrée pour en faire un vecteur de taille 32 x 32 = 1024.
Supposons que nous souhaitions réaliser une classification parmi dix classes possibles. Nous voulons donc obtenir dix valeurs en sortie, chacune représentant la probabilité que l’image appartienne à une des classes. Nous aurons donc besoin de dix neurones dans la couche de sortie de notre réseau.
De plus, supposons que notre réseau contient une unique couche cachée, elle aussi avec 10 neurones.
Chaque neurone de la couche cachée va effectuer une somme pondérée sur l’ensemble des pixels de l’image d’entrée. Pour cela, chaque neurone de la couche cachée aura donc 1024 poids à optimiser. Cette couche contiendra donc au total 1024 x 10 = 10 240 poids.
De plus, chacun des dix neurones de la couche de sortie va lui aussi effectuer une somme pondérée sur l’ensemble des sorties de la couche cachée. Pour cela, chaque neurone de la couche de sortie aura 10 poids à optimiser, soit 10 x 10 = 100 poids au total.
Au total, nous aurons besoin d’optimiser 10 240 + 100 = 10 340 poids, pour un réseau contenant une unique couche cachée, ce qui est énorme.
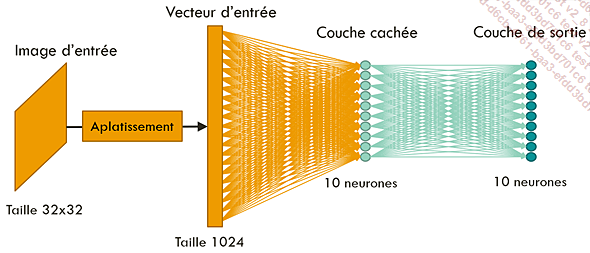
Réseau prenant en entrée...
Fonctionnement détaillé de chaque type de couche
1. Architecture générale d’un réseau de neurones à convolution
Dans cette partie, nous allons voir comment est construit un réseau de neurones à convolution.
Comme les réseaux de neurones profonds conventionnels, ce type de réseau est constitué d’un empilement de couches.
Nous avons vu dans le chapitre précédent qu’un réseau de neurones profond n’était constitué que de couches denses. Dans un réseau de neurones à convolution, nous trouvons également des couches de convolution, des couches d’agrégation, et des couches de normalisation par lot.
Dans la suite de ce chapitre, nous allons détailler le fonctionnement de chaque type de couche. Nous décrirons également comment ajouter ces couches à un réseau séquentiel, déjà introduit dans le chapitre précédent, avec Keras.
2. Couches de convolution
a. Fonctionnement d’un filtre de convolution
La couche de convolution est constituée de plusieurs filtres de convolution.
Un filtre de convolution est une petite image carrée, de taille impaire, qui glisse sur tous les pixels de l’image originale pour obtenir une nouvelle image.
Cette image est obtenue de la manière suivante : à chaque position du filtre, nous additionnons les produits des valeurs de l’image et du filtre, ce qui donne un scalaire. Ce scalaire définit la valeur du pixel de l’image résultat à la position centrale du filtre.
C’est pour cette raison qu’il est nécessaire que la taille du filtre soit impaire ; il serait impossible de définir le pixel central dans le cas contraire.
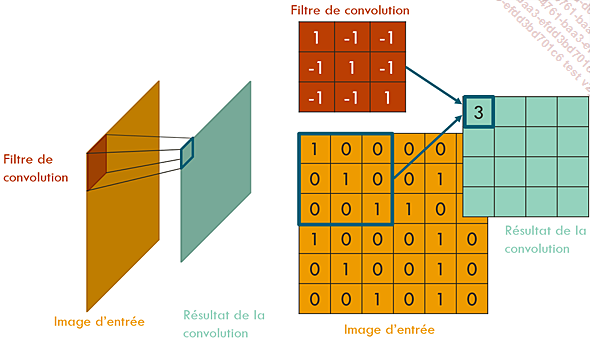
Résultat de la convolution à la première position du filtre. Seule la valeur du premier pixel de l’image de sortie a été calculée.
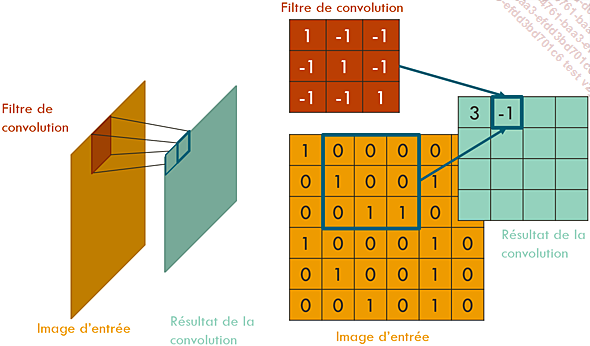
Résultat de la convolution à la deuxième position du filtre. Les valeurs des deux premiers pixels de l’image de sortie ont été calculées.
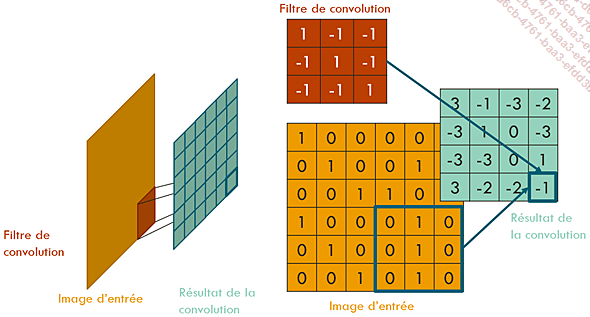
Résultat de la convolution à la dernière position du filtre. À cette étape, les valeurs de tous les pixels de l’image de sortie ont été calculées.
 l’opération...
l’opération...Étapes de l’apprentissage des réseaux de neurones convolutionnels
L’entraînement d’un réseau de neurones convolutionnel se fait en plusieurs étapes qui sont proches de celles requises pour l’entraînement d’un réseau de neurones profond.
Tout d’abord, il est nécessaire de séparer l’ensemble de données en plusieurs sous-ensembles : les données d’entraînement, les données de validation, et les données de test. Cette étape est strictement identique, qu’elle soit réalisée pour un classifieur linéaire, pour un réseau de neurones profond ou pour un réseau convolutionnel. Elle a déjà été décrite dans le chapitre Classifieurs linéaires, et nous n’en reparlerons pas dans ce chapitre.
Il faut ensuite définir divers hyperparamètres du réseau, comme la fonction d’activation, l’architecture du réseau et divers paramètres de l’optimisation. Nous avons détaillé au chapitre précédent comment définir les hyperparamètres nécessaires pour un réseau de neurones profond.
Certains hyperparamètres, comme le type de fonction d’activation, le taux d’apprentissage, la méthode d’optimisation, le taux d’extinction de neurones...
Sélection des hyperparamètres
1. Liste des hyperparamètres et stratégie de sélection
Nous avons détaillé au chapitre précédent l’influence de la valeur de chaque hyperparamètre sur les performances du réseau final. Cette influence respective reste inchangée pour les réseaux convolutionnels.
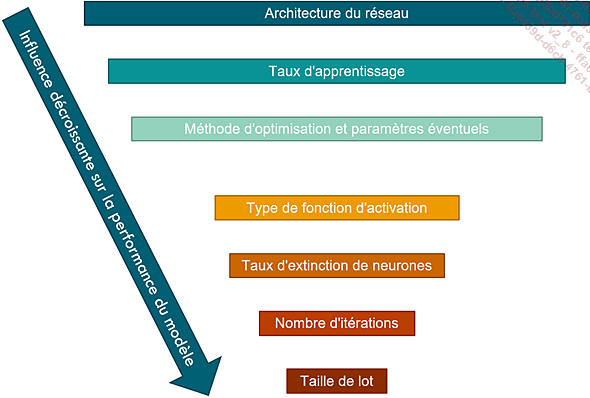
Hyperparamètres d’un réseau de neurones profond classés selon leur influence sur la performance du modèle final
Cependant, la manière de choisir deux groupes de paramètres (l’architecture du réseau et la taille de lot) diffère.
Détaillons la manière dont chacun de ces groupes de paramètres peut être sélectionné.
2. Choix de la structure du réseau
a. Facteur de sous-échantillonnage et nombre de couches
Les performances d’un réseau sont meilleures lorsque les dimensions spatiales des cartes d’activation sont de plus en plus petites, tandis que leur profondeur augmente, et lorsque ces changements sont progressifs.
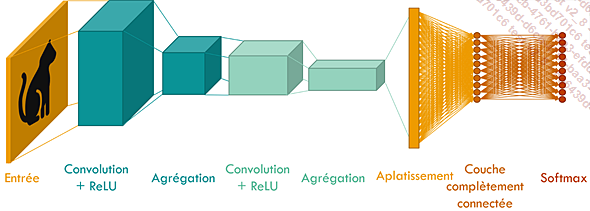
Représentation de l’évolution des cartes d’activation au fur et à mesure de l’avancement dans le réseau de neurones convolutionnel. Les dimensions spatiales se réduisent, tandis que la profondeur augmente.
Cette constatation a plusieurs conséquences sur l’architecture du réseau....
Prétraitement des images
1. Augmentation de données
L’augmentation de données (ou data augmentation, en anglais) a pour but d’augmenter la quantité et la diversité des images utilisées pour entraîner un modèle, ce qui permet d’accélérer la convergence et d’améliorer les performances.
En pratique, elle consiste à appliquer des transformations aux images qui ne vont pas modifier les étiquettes, par exemple :
-
des translations
-
des rotations
-
des modifications de couleur ou de niveau de gris
-
des retournements verticaux ou horizontaux
-
etc.

Modification de l’image sans modification de l’étiquette pour augmenter les données
Le choix de ces transformations dépend de votre application. Ainsi, pour un classifieur qui cherche à distinguer les mains droites des mains gauches, l’application d’un retournement horizontal à l’image risquerait de modifier l’étiquette. Une telle transformation ne devrait donc pas être appliquée.
Il est important de noter que l’augmentation de données ne devrait être réalisée que sur les données d’entraînement, et jamais sur les données de validation. Ceci vous permet de vous assurer que les performances obtenues sur les données de validation sont représentatives des performances...
Mise en pratique : créer et entraîner un réseau de neurones avec Tensorflow et Keras
Avec un classifieur linéaire, nous avions pu distinguer des photos de chiens de photos de chats avec une précision de 71,5 %.
Nous allons maintenant créer et entraîner un réseau de neurones à convolution pour améliorer ce classifieur.
Le code Keras utilisé pour créer et entraîner ce réseau de neurones est disponible en téléchargement, dans le notebook reseaux_de_neurones_a_convolution.ipynb.
Conclusion
Dans ce chapitre, nous avons détaillé l’architecture des réseaux de neurones à convolution, et la manière dont ils étaient entraînés.
Cependant, en pratique, optimiser les poids d’un réseau de neurones à convolution se révèle délicat. Du fait de leur complexité, ces réseaux sont de plus difficiles à déboguer. Ils peuvent également souffrir de biais, et leur entraînement a un impact carbone non négligeable.
Certaines bonnes pratiques permettent cependant d’améliorer les performances des réseaux, limiter les biais, et réduire l’impact carbone de leur entraînement. Le prochain chapitre leur sera consacré.
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations



