Les concepts fondamentaux

1. Le système binaire

Le système binaire est essentiel car c’est l’unique représentation que les systèmes informatiques sont en mesure d’interpréter.

Ainsi, qu’il s’agisse de caractères alphanumériques ou de représentations graphiques, un système informatique ne peut les traiter qu’à la condition qu’ils lui soient soumis sous forme binaire.

Cette limitation des systèmes informatiques est due au fait qu’il ne s’agit, après tout, que de systèmes électroniques qui ne connaissent que les deux états fondamentaux : 0 et 1.

Dans le cadre des réseaux informatiques, le système binaire fait partie des concepts fondamentaux à maîtriser car il sert de base à un certain nombre de fonctions importantes comme l’adressage.

Le système binaire est une méthode de numération qui semble très simple puisqu’elle ne dispose que de deux valeurs : 0 et 1.

Il est également appelé système en base 2 (puisqu’il ne contient que deux possibilités de valeurs). On dénomme "bit" un chiffre binaire, un bit ne peut donc avoir que deux valeurs : 0 ou 1.

Si ce système ne comporte que deux valeurs, comment est-il possible de représenter des valeurs décimales voire des caractères alphanumériques ? Réponse : la combinaison de plusieurs bits permet d’exprimer des valeurs plus complexes. 

Il est important de comprendre également la notion d’octet (byte en anglais). Un octet est le regroupement de 8 bits dans le but de coder une information. Chacun de ces 8 bits pouvant se caractériser en deux états différents (0 ou 1), il est alors possible de coder 2⁸ combinaisons différentes soit 256 valeurs.

Mathématiquement plusieurs méthodes sont valables pour coder un chiffre en binaire.

Une première méthode est de diviser le nombre à convertir par le nombre de valeurs possibles d’un caractère binaire (un bit), soit 2.

1. Le système international

Les préfixes SI (Système International) utilisent les puissances de 1 000 comme c’est le cas pour les unités de mesure de poids ou de distance. Donc 1 kilomètre est équivalent à 1 000 mètres tout comme 1 kilogramme est équivalent à 1 000 grammes.

Ainsi le préfixe "Kbit" pour "kilobit" représente une valeur en millier (ou 10³), les connexions 56k étaient donc en mesure d’envoyer 56 000 bits par seconde.

Lorsque l’unité "kilobit" n’est plus suffisante pour simplifier l’écriture, on utilise alors "Mbit" pour "mégabit" qui représente une valeur en millions ou 10⁶. Cela signifie par exemple que lorsqu’on parle d’une connexion ADSL à 2 Mbps, on estime alors que le débit maximal de la ligne permet d’envoyer 2 000 000 bits par seconde ou encore 2 000 Kbps.

De nos jours les réseaux locaux atteignent facilement des vitesses dix fois supérieures, on utilise alors le préfixe "Gb" pour...

1. Le code, définition générale

Un code est une règle qui permet de convertir une information donnée sous une autre forme. On pense alors immédiatement aux messages codés qui sont utilisés pour tenter de conserver une information la plus confidentielle possible. Certains furent célèbres pendant les guerres, comme le code Enigma et le code de Lorenz. Mais un code n’est pas forcément utilisé dans un contexte de sécurité.

Exemples de codes autres que ceux du domaine informatique :

Code de la route : un message correspond à un panneau.

Code des couleurs : à chaque couleur correspond un chiffre (Ne Mangez Rien Ou Jeûnez Voilà Bien Votre Grande Bêtise - Noir Marron Rouge Orange Jaune Vert Bleu Violet Gris Blanc - 0 1 2 3 4 5 6 7 8 9).

Code Braille : à chaque caractère de l’alphabet correspond un ensemble de points.

Code Morse : à chaque caractère correspond une séquence de sons.

Code pénal : à un délit correspond une peine.

2. La longueur du code

Deux éléments binaires offrent quatre combinaisons [00, 01, 10, 11] susceptibles de coder quatre symboles. Trois éléments binaires offrent huit combinaisons [000, 001, 010, 011, 100, 101, 110, 111] susceptibles de coder huit symboles.

Pour coder N symboles, n bits sont nécessaires avec N ≤ 2n. Combien de symboles faut-il coder ? Pour coder quoi ?

L’expert réseau contribue à transporter l’information sans chercher à l’interpréter. S’étendre sur les codes selon la nature de l’information - voix, données, images - est certainement captivant mais sort un peu du cadre de ce chapitre.

Pour illustrer la manière dont fonctionnent les codes et comment ils sont appliqués au monde informatique, le codage des caractères...

1. L’algèbre de Boole

Les opérations booléennes sont des opérations logiques effectuées sur des valeurs fournies que l’on appelle des valeurs d’entrée. Ces opérations viennent initialement des mondes de la logique et de l’électronique.

Elles sont régulièrement utilisées en réseau dans des opérations qui consiste à déterminer une action en fonction des valeurs d’entrée.

Ces opérations, dont les valeurs d’entrée sont des adresses IP et des masques de sous-réseaux, sont la base de décisions.

Les exemples présentés ici sont des exemples simples à deux valeurs d’entrée. Bien entendu il est possible d’utiliser l’algèbre de Boole avec plus de deux valeurs d’entrée.

2. La fonction AND

La fonction AND est aussi dénommée "produit logique". Il s’agit de comparer les valeurs afin de construire la table de vérité suivante, où "a" et "b" sont les valeurs d’entrée et "L" le résultat.

Dans cette opération, si l’une des valeurs d’entrée est 0 alors le résultat est 0.

Cette opération de produit logique doit être associée à l’idée de contacts placés en série, au mot-clé « ET », au signe « x » ou « ⋅ ».

Dans l’exemple suivant, les interrupteurs a et b ont 0 pour valeur (ils sont ouverts), le résultat de la lampe L est 0 (elle est éteinte). Il faut donc que les deux interrupteurs soient fermés pour que la lampe soit alimentée.

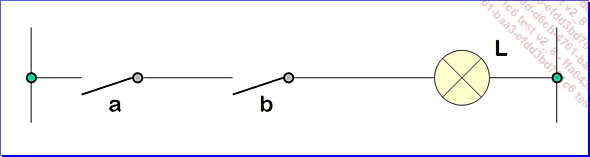
Schéma AND

Le symbole ANSI (American National Standard Institute) de l’opération AND est le suivant :

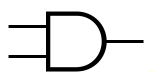
Symbole AND

3. La fonction OR

La fonction OR est aussi dénommée "somme logique", la table de vérité de l’opération OR est la suivante :

Dans cette opération logique, si l’une des valeurs d’entrée est 1 alors le résultat est 1.

Cette opération de somme logique...