Présentation

Pour s’adapter aux nouvelles technologies logicielles, notamment à la percée des langages orientés objet et du langage UML, la méthode Merise a dû s’enrichir et évoluer.

Au cours de ce chapitre, nous allons étudier les éléments majeurs des extensions Merise, appelées aussi Merise/2.

Les identifiants relatifs sont traités au chapitre Le modèle conceptuel des données.

L’héritage (ou la généralisation - spécialisation)

Commençons directement par un exemple.

Une maison de santé reçoit des patients.
Deux types de personnel sont salariés : les médecins qui réalisent les consultations et les infirmiers qui administrent les soins.
Les médecins ont une spécialisation (médecin du sport, gérontologue…) et un tarif à l’acte.
Les infirmiers ont des primes d’astreinte.
Les patients sont juste référencés par leur numéro de Sécurité sociale.

Imaginons le MCD suivant :

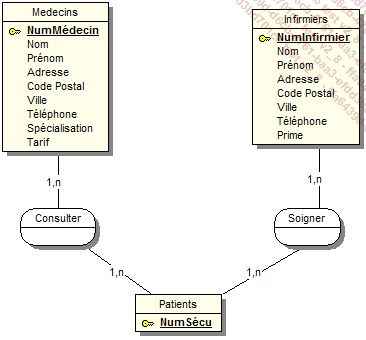
Ce MCD pourrait aussi être représenté sous cette forme :

Si nous examinons ces deux solutions, qui sont correctes dans les faits, nous nous rendons compte qu’elles présentent des inconvénients structurels.

Dans le premier modèle conceptuel, il y a des attributs dupliqués entre les deux entités Médecins et Infirmiers (Nom, Prénom, Adresse…).

Dans le deuxième modèle conceptuel, certains attributs seront vides :

Spécialisation et Tarif pour les infirmiers
Prime pour les médecins

Pour résoudre ces problèmes, nous allons utiliser l’héritage.

Le principe de l’héritage est de factoriser les propriétés identiques dans une entité commune....

Les contraintes ensemblistes

Les extensions du modèle entité-association permettent de représenter des contraintes sur des ensembles d’occurrences d’entités ou d’associations.

L’entité concernée par la contrainte est appelée le pivot de la contrainte.

L’ensemble des contraintes est formé à partir de deux contraintes de base :

La contrainte de couverture : toute occurrence de l’entité générique appartient au moins à l’un des sous-types.
La contrainte de disjonction : toute occurrence de l’entité générique doit appartenir à un seul sous-type. Les sous-types sont ainsi mutuellement exclusifs.

Exemple

Un employé est soit un employé interne soit un employé d’une SSII, mais pas les deux.

Si nous combinons ces deux types de contraintes, nous obtenons les quatre cas suivants :

Une occurrence du surtype n’appartient à aucun sous-type, ou appartient à un sous-type ou à plusieurs sous-types. Il n’y a donc ni couverture ni disjonction. Dans ce cas-là, il n’y a aucune contrainte à formaliser.
Une occurrence du surtype appartient toujours à un sous-type, éventuellement à plusieurs sous-types. Dans ce cas, il y a donc couverture, mais pas de disjonction. C’est formalisé par une contrainte...

La formalisation des contraintes entre associations

Nous avons vu comment formaliser les contraintes entre entités, voyons maintenant comment formaliser des contraintes entre associations.

Nous retrouvons les quatre contraintes précédemment décrites pour les sous-types :

contrainte de totalité : couverture + non-disjonction
contrainte de partition : couverture + disjonction
contrainte d’exclusion : non-couverture + disjonction
aucune contrainte : non-couverture + non-disjonction

À ces contraintes s’ajoutent :

Une contrainte d’égalité ou de simultanéité, noté = ou S : toute occurrence qui participe à l’association A participe également à l’association B.
Une contrainte d’inclusion, notée I : toutes les occurrences d’une association A sont également des occurrences d’une association B.

Étudions cela avec quelques exemples.

1. La totalité (couverture + non-disjonction)

Prenons l’exemple d’un apprenti qui travaille dans une entreprise et se forme dans un centre de formation :

Si nous interprétons la contrainte d’intégrité, nous voyons qu’un apprenti participe à au moins une des deux associations, car il y a couverture et non-disjonction. En fait, soit il travaille dans une entreprise, soit il apprend dans...

Agrégation sur les associations (ou associations d’associations)

Dans la compagnie d’aviation Vol’toujours, les pilotes font voler des avions dans différents pays. Mais un avion pour un pays donné n’est piloté que par un seul pilote. Cette règle de gestion est absurde, mais elle va nous permettre d’illustrer l’agrégation.

Voici un modèle conceptuel exprimant parfaitement le fait que les pilotes peuvent faire voler des avions dans différents pays. Mais la règle de gestion n’est pas intégrée et il est difficile de la formaliser sans l’utilisation de l’agrégation. Voici une solution intégrant la représentation de l’agrégation :

L’agrégation consiste à percevoir comme un objet unique l’association de plusieurs autres objets. Ici, ce qui est encadré représente un ensemble.

D’autres représentations peuvent être proposées, mais elles seront moins explicites que celle vue précédemment.