Décision en avenir certain : l'optimisation

Principe

De manière générale, un problème d’optimisation est un problème dans lequel le décideur doit agir sur des variables dans le but de maximiser (ou de minimiser selon le cas) un résultat lié directement ou indirectement à ces variables.

La plupart des problèmes d’optimisation doivent aussi respecter des contraintes, c’est-à-dire un nombre maximum ou minimum à ne pas dépasser relatif à des problèmes économiques, comme par exemple une contrainte budgétaire ou simplement logique (il n’est par exemple pas possible de produire une quantité négative).

Il est possible de décomposer un problème d’optimisation en trois étapes distinctes.

La première étape est la phase de construction du modèle. Nous allons y déterminer quels sont les variables, les objectifs et les contraintes puis les retranscrire sous forme algébrique ou tout du moins, dans notre cas, sous la forme d’un tableau Excel comportant des formules matérialisant les liens mathématiques entre les différents éléments du modèle. 

La deuxième étape est la phase de résolution du modèle d’optimisation c’est-à-dire la détermination de la solution optimale parmi toutes les solutions respectant les contraintes...

Cas pratique n° 1 : optimisation du nombre de produits à fabriquer

La société Elena, spécialiste dans la création et la distribution d’articles végans, aimerait mettre au point une nouvelle gamme de pulls 50 % coton et 50 % chanvre.

Trois modèles sont à l’étude. La société Elena souhaiterait savoir combien elle devrait fabriquer de pulls pour chacun des modèles afin de maximiser son résultat en fonction des éléments suivants :

Ressources nécessaires 

Le modèle 1 nécessite 2,5 unités de chanvre, 2,5 unités de coton et 0,75 heure de main-d’œuvre. 

Le modèle 2 nécessite 2,8 unités de chanvre, 3,5 unités de coton et 1 heure de main-d’œuvre.

Le modèle 3 nécessite 4 unités de chanvre, 5 unités de coton et 2 heures de main-d’œuvre.

Contraintes

Ressources maximums de chanvre : 1 000 unités

Ressources maximums en coton : 1 500 unités

Ressources maximums en main-d’œuvre : 400 heures

Résultat par unité

Pour le modèle 1 : 6,5 €

Pour le modèle 2 : 7,5 €

Pour le modèle 3 : 11 €

Première étape : construction du modèle

Il est possible de modéliser ce problème de la manière suivante :

Variables 

x1, x2 et x3 sont les quantités de modèles 1, 2 et 3 à fabriquer.

Fonction objectif à maximiser

La fonction F correspond au résultat total : F(x1, x2, x3) = 6,5x1 + 7,5x2 + 11x3  

Nous recherchons donc :

max[F(x1, x2, x3) = 6,5x1 + 7,5x2 + 11x3]

Contraintes 

Il s’agit de la disponibilité de chacune des ressources, nous pouvons écrire :

Chanvre : 2,5x1 + 2,8x2 + 4x3 ≤ 1 000

Coton : 2,5x1 + 3,5x2 + 5x3 ≤ 1 500

Main-œuvre : 0,75x1 + 1x2 + 2x3 ≤ 400

Ces éléments ont été retranscrits...

Cas pratique n° 2 : optimisation du choix des projets

Le but de cette application est d’utiliser la possibilité d’utiliser des contraintes binaires dans le solveur d’Excel.

Cette année, dans le cadre de son développement, la société Elena a le choix entre 10 projets. Cependant, du fait de contraintes budgétaires et de contraintes en moyens humains, la société est dans l’obligation d’effectuer une sélection dans les projets disponibles tout en gardant à l’esprit la recherche d’un résultat optimal.

Les différents projets ainsi que leur coût, leur chiffre d’affaires et les heures de main-d’œuvre nécessaires sont répertoriés dans le tableau suivant :

Cependant, la société Elena ne dispose que de 20 000 € de budget et de 100 heures de main-d’œuvre disponibles.

Bien entendu, la société ne peut accepter de demi-projet. Une fois accepté, le projet doit aller à son terme.

Vous retrouverez cet exemple dans l’ongle opt_projet du fichier solver_projet.xlsx. Sa résolution se trouve dans l’onglet opt_projet_resolution.

Première étape : construction du modèle

Pour réaliser cette optimisation, nous allons utiliser une technique appelée variable muette (dummy variable en anglais). Cette technique est semblable à du code binaire. Elle consiste à utiliser le nombre 1 si le projet est accepté ou le code 0 si le projet est refusé.

Le tableau servant de cadre à notre optimisation se présente de la manière suivante :

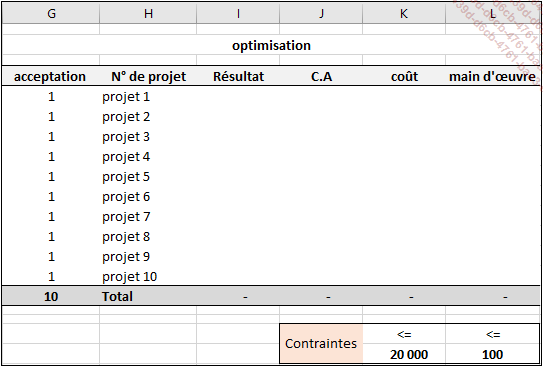
Les zones nommées

Par défaut, tous les projets sont codés à 1 dans la plage de cellules G5:G14 pour pouvoir vérifier par la suite si les formules qui vont être mises en place fonctionnent correctement.

Cette plage a été nommée au préalable acceptation.

Le résultat total se trouve dans la cellule I15, cette cellule a été nommée resultat_total.

Le coût total se trouve dans la cellule K15, cette cellule...