Les probabilités
Les probabilités conditionnelles
Si A et B sont deux événements d’un même univers U, on appelle probabilité de B sachant A et on note PA(B) la probabilité que l’événement B se réalise quand on sait déjà que l’événement A s’est réalisé. On dit que cette probabilité est une probabilité conditionnelle.
1. Une simulation pour conjecturer
On lance deux dés à six faces bien équilibrés 10 000 fois de suite et on s’intéresse aux événements suivants :
-
L’événement A se produit quand la somme S des points est impaire.
-
L’événement B se produit quand la somme S des points est strictement supérieure à 7.
-
L’événement
se produit quand la somme des points est impaire ET strictement supérieure à 7.
1. Le premier programme détermine la fréquence de l’événement B quand on lance les dés 10 000 fois de suite.
# Fréquence de l'événement B
from random import*
n=0
for i in range(1,10001):
dé1=randint(1,6)
dé2=randint(1,6)
s=dé1+dé2
if s>7:
n=n+1
f=n/10000
print("Fréquence de l'événement B=",f) Pour une série de 10 000 lancers successifs des deux dés, on obtient une fréquence de 0,4207. Comme le nombre de lancers est très grand, on peut assimiler cette fréquence à la probabilité de réalisation de l’événement B.
La formule de Bayes
Connaissant la probabilité d’un événement pour chacune de ses causes possibles, la formule de Bayes permet de calculer la probabilité de chacune de ces causes lorsque l’événement se réalise.
1. Historique
Thomas Bayes (1702-1761) était un pasteur et mathématicien anglais qui défendait les idées de Newton. Ses travaux sur les probabilités n’ont été publiés qu’en 1763, deux ans après sa mort. De façon indépendante, Pierre-Simon de Laplace (1749-1827) a exposé les mêmes résultats dans son Essai philosophique sur les probabilités publié en 1774.

Thomas Bayes (1702-1761)
2. La formule de Bayes
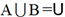 et
et 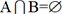 . Il en résulte que tout événement
de U appartient soit à A soit à B. En observant
que les événements
. Il en résulte que tout événement
de U appartient soit à A soit à B. En observant
que les événements 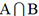 et
et 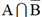 sont disjoints
et ont pour réunion A, on peut écrire
sont disjoints
et ont pour réunion A, on peut écrire 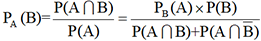 . Cette relation, qui constitue la formule de Bayes,
peut s’écrire également
. Cette relation, qui constitue la formule de Bayes,
peut s’écrire également 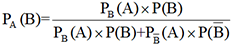 .
.3. Une première simulation
On dispose de trois urnes identiques. La première contient 2 boules blanches et 1 noire. La deuxième contient 3 boules blanches et 1 noire. La troisième contient 2 boules blanches et 2 noires. On choisit une urne au hasard et on en tire une boule. On peut déterminer la probabilité de tirer une boule blanche avec ce programme qui simule une série de 1 000 expériences :
from random import*
compteur=0
for n in range(1,1000):
blanche=0
# Choix de l'urne
numéro=randint(1,3)
if numéro==1:
x=randint(1,3) ...L’espérance et l’écart-type d’une variable aléatoire discrète
Les valeurs prises par une variable aléatoire sont réparties autour de son espérance mathématique, notion qui joue donc le rôle d’une moyenne. L’écart-type d’une variable aléatoire mesure la dispersion des valeurs de cette variable autour de son espérance.
1. Variables aléatoires discrètes
Grandeur numérique attachée à une expérience aléatoire, une variable aléatoire peut prendre diverses valeurs qui ne dépendent que de cette expérience aléatoire. Si le nombre de ces valeurs est fini, on dit que la variable est discrète. Par exemple, quand on lance deux dés à 6 faces, la somme des points obtenus définit une variable aléatoire discrète X qui peut prendre 11 valeurs comprises entre 2 et 12. L’événement X=5 est réalisé dans 4 cas mais l’événement X=12 dans un seul.
2. Variables aléatoires et lois de probabilité
 . On écrit alors P(X=k)=
. On écrit alors P(X=k)= .
.3. Espérance mathématique d’une variable aléatoire
Soit X une variable aléatoire discrète qui prend les valeurs x1, x2, x3, ….., xn avec les probabilités respectives p1, p2, p3, ….., pn. Par définition...
La loi binomiale
Soit k et n deux entiers tels que 0 ≤ k ≤ n. La loi binomiale permet de calculer la probabilité d’obtenir exactement k succès dans une suite de n expériences de Bernoulli, chaque succès se produisant avec la probabilité p.
1. Expériences et schémas de Bernoulli
Une expérience aléatoire qui n’a que deux issues possibles, un succès ou un échec, est appelée une expérience de Bernoulli. La répétition de plusieurs expériences de Bernoulli constitue un schéma de Bernoulli. La figure qui suit montre l’arbre des possibilités qui caractérise un schéma de Bernoulli constitué d’une succession de quatre épreuves identiques. Un succès est noté S, un échec est noté E.
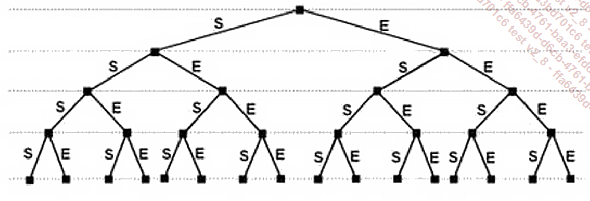
Cet arbre permet de déterminer le nombre des succès obtenus quand on fait se succéder 1, 2, 3 ou 4 épreuves. Pour cela, on utilise les deux règles suivantes :
-
La probabilité du résultat indiqué par un chemin quelconque de l’arbre des possibles est le produit des probabilités des événements qui se succèdent sur ce chemin.
-
La probabilité d’un événement est la somme des probabilités associées aux chemins qui permettent de réaliser cet événement.
2. Étude d’un exemple
Utilisons cet arbre pour déterminer la probabilité de l’événement obtenir k fois un 6 en lançant un dé à 6 faces bien équilibré 4 fois de suite, pour 0 ≤ k ≤ 4.
|
Événement à obtenir en 4 lancers successifs |
Probabilité de l’événement |
|
4 fois le 6 |
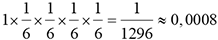 |
|
3 fois le 6 |
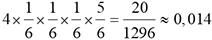 |
|
2 fois le 6 |
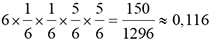 |
|
1 fois le 6 |
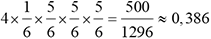 |
|
0 fois le 6 |
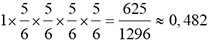 |
La loi de Poisson
La loi de Poisson est une loi discrète de probabilité qui s’applique aux évènements rares, c’est-à-dire peu fréquents : pannes d’une machine, accidents de voiture, décès accidentels par exemple.
1. Historique
En 1837, trois ans avant sa mort, le mathématicien et physicien français Denis Siméon Poisson (1782-1840) a publié ses Recherches sur la probabilité des jugements en matière criminelle et en matière civile. Dans cet ouvrage, il étudie les probabilités de voir un innocent condamné par un jury pour un crime qu’il n’aurait pas commis ou, à l’inverse, de voir un coupable véritable acquitté par la justice. Ce travail l’amène à formuler une nouvelle loi de probabilité qui, plus tard, portera son nom.
2. Expression de la loi de Poisson
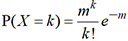 . Le paramètre m est
toujours une moyenne : un nombre moyen, une fréquence moyenne,
etc. On démontre que E(X)=(X)=m.
Le programme qui suit calcule P(X=k).
. Le paramètre m est
toujours une moyenne : un nombre moyen, une fréquence moyenne,
etc. On démontre que E(X)=(X)=m.
Le programme qui suit calcule P(X=k).# Loi de Poisson. Calcul des probabilités P(X=k)
m=eval(input("Valeur de m ?"))
k=eval(input("Valeur de k ?"))
from math import*
F=factorial(k)
proba=(m**k)*exp(-m)/F
print("P(X)=",proba) Avec m=0,516 et k=0, on obtient les résultats suivants :
Valeur de m ? 0.516
Valeur de k ? 0
P(X)= 0.596903392674358 En modifiant légèrement le programme précédent, on peut calculer P(X ≤ k).
# Loi de Poisson. Calcul des probabilités P(X<=k)
m=eval(input("Valeur de m ?"))
k=eval(input("Valeur...Les variables aléatoires continues
Contrairement aux variables aléatoires discrètes qui prennent un nombre fini de valeur, les variables aléatoires continues prennent leurs valeurs dans des intervalles de R. De ce fait, elles peuvent prendre une infinité de valeurs.
1. Historique
Considérée pendant longtemps comme une partie des mathématiques appliquées, la théorie des probabilités prend un nouvel essor au début du XXe siècle grâce à l’introduction de nouveaux concepts comme celle de variable aléatoire continue opposée à la notion de variable aléatoire discrète. Les travaux d’Émile Borel (1871-1956) et ceux d’Henri Lebesgue (1875-1941) ont permis de rattacher les probabilités à la théorie de l’intégration. Certaines lois de probabilité, qui avaient été définies plus ou moins empiriquement, ont alors été définies rigoureusement. Axiomatisée par les travaux d’Andreï Kolmogorov (1903-1987), la théorie des probabilités est devenue une branche des mathématiques à part entière en 1933.

Émile Borel (1871-1956)
2. Qu’est-ce qu’une variable aléatoire continue ?
Imaginons que l’on verse de l’eau en quantité aléatoire dans un récipient cylindrique de 20 cm de hauteur. Désignons par X (en cm) la hauteur atteinte par l’eau une fois qu’elle a été versée.
Cette variable est une variable aléatoire qui peut prendre une infinité de valeurs dans l’intervalle [0;20]. On dit que c’est une variable aléatoire continue.
La loi exponentielle
Comme son nom l’indique, cette loi de probabilité utilise la fonction exponentielle de base e=2,718…. comme fonction de densité de probabilité.
1. À quoi sert cette loi ?
En pratique, la loi exponentielle concerne toujours des temps d’attente, des durées de vie ou encore des durées de fonctionnement sans panne. Si X est une variable aléatoire qui suit la loi exponentielle, elle s’exprime en secondes ou en minutes ou en jours ou en mois ou encore en années.
2. Définition
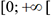 la fonction f définie
par
la fonction f définie
par 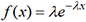 . La figure qui suit montre
les courbes représentatives de la fonction f pour trois valeurs différentes
du paramètre λ.
. La figure qui suit montre
les courbes représentatives de la fonction f pour trois valeurs différentes
du paramètre λ.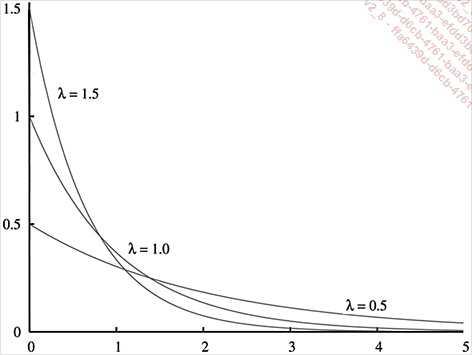
Toutes ces fonctions sont positives et décroissantes et on a toujours f(0)= λ.
3. Espérance et variance d’une loi exponentielle.
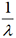 . Sa variance V(X)
est égale à
. Sa variance V(X)
est égale à 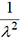 .
.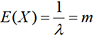 d’où
d’où 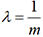 . Considérons par exemple les machines à laver
de marque Z qui connaissent en moyenne leur première panne
au bout de 2,5 années de fonctionnement. Soit T (en années) la variable
aléatoire égale au temps qu’il faut attendre après
la mise en service d’une machine neuve de cette marque pour que
survienne la première panne. Si on admet que T suit une loi exponentielle de
paramètre λ, on a
. Considérons par exemple les machines à laver
de marque Z qui connaissent en moyenne leur première panne
au bout de 2,5 années de fonctionnement. Soit T (en années) la variable
aléatoire égale au temps qu’il faut attendre après
la mise en service d’une machine neuve de cette marque pour que
survienne la première panne. Si on admet que T suit une loi exponentielle de
paramètre λ, on a 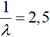 d’où...
d’où...La loi normale
Parfois nommée loi de Gauss-Laplace, cette loi de probabilité a été proposée au XVIIIe siècle par Pierre-Simon de Laplace (1749-1827) et au début du XIXe siècle par Carl Friedrich Gauss (1777-1855). À l’origine de leurs travaux, il y a l’étude de la distribution des erreurs qui entachent inévitablement les mesures physiques. La loi normale joue un rôle important dans les calculs de probabilité et de statistique.
 Pierre-Simon de Laplace (1749-1827) |
 Carl Friedrich Gauss (1777-1855) |
1. Définition
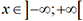 par
par 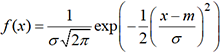 . Cette fonction
est positive et atteint son maximum pour x=m.
Sa courbe représentative est la célèbre « courbe
en cloche » qui est symétrique par rapport à la
parallèle à l’axe des y qui
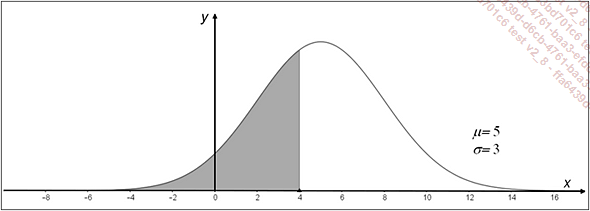
passe par m. Voici par exemple
la courbe qui représente la densité de probabilité de
la loi normale de moyenne m=5
et d’écart-type σ=3.
Sur la figure, l’aire de la partie coloriée représente
la probabilité P(X ≤ 4).
. Cette fonction
est positive et atteint son maximum pour x=m.
Sa courbe représentative est la célèbre « courbe
en cloche » qui est symétrique par rapport à la
parallèle à l’axe des y qui
passe par m. Voici par exemple
la courbe qui représente la densité de probabilité de
la loi normale de moyenne m=5
et d’écart-type σ=3.
Sur la figure, l’aire de la partie coloriée représente
la probabilité P(X ≤ 4).En raison de la symétrie de la courbe, on peut observer qu’on a toujours P(X ≤ μ) = P(X ≥ μ) = 0,5
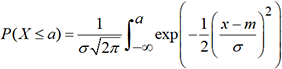 .
.2. Loi normale réduite...
Loi normale et jugements statistiques
Les propriétés de la loi normale permettent de déterminer les intervalles de fluctuation et les intervalles de confiance qui constituent la base du jugement statistique.
1. Intervalle de fluctuation d’une moyenne
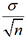 . On peut alors se ramener à une série
normale réduite en posant
. On peut alors se ramener à une série
normale réduite en posant 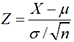 . Pour trouver un nombre positif α tel que P( α < Z < α) = 0,95,
on peut utiliser le programme de la section Calcul inverse de ce
chapitre. On obtient a=1,96. Par suite, P(-1,96 < Z < 1,96) = 0,95.
. Pour trouver un nombre positif α tel que P( α < Z < α) = 0,95,
on peut utiliser le programme de la section Calcul inverse de ce
chapitre. On obtient a=1,96. Par suite, P(-1,96 < Z < 1,96) = 0,95.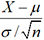 , on peut alors écrire
, on peut alors écrire 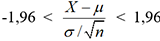 . En pratique, si on a n>30
on peut dire qu’il y a 95 chances sur 100 pour que la moyenne d’un échantillon
de n valeurs appartienne à l’intervalle
. En pratique, si on a n>30
on peut dire qu’il y a 95 chances sur 100 pour que la moyenne d’un échantillon
de n valeurs appartienne à l’intervalle 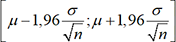 . Cet intervalle est appelé l’intervalle
de fluctuation au seuil de 95% de la moyenne des échantillons.
. Cet intervalle est appelé l’intervalle
de fluctuation au seuil de 95% de la moyenne des échantillons.Le même raisonnement pourrait être fait au seuil de 99%. Il suffirait de remplacer 1,96 par 2,58.
Le programme suivant calcule les bornes a et b de l’intervalle de fluctuation de la moyenne des échantillons de taille n au seuil de 95%, ces échantillons étant extraits d’un ensemble de moyenne μ et d’écart-type...
 Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

