Dérivation numérique et équations différentielles
Dérivée d’une fonction numérique
Le concept de dérivée d’une fonction numérique s’est dégagé progressivement en plusieurs phases. Né au XVIIe siècle de l’étude des tangentes à une courbe, le concept n’a été formulé sous la forme actuelle qu’au XIXe siècle.
1. Historique
Au XVIIe siècle, Fermat (1601-1665) met au point une méthode pour trouver le maximum ou le minimum d’une fonction. Il montre que l’existence d’un extremum implique l’annulation de ce qu’on appellera plus tard la dérivée de la fonction étudiée, mais celle-ci n’apparaît véritablement qu’avec le calcul infinitésimal, dont la paternité est attribuée conjointement à Newton (1642-1727) et à Leibniz (1646-1716). Newton nomme fluxion ce que nous appelons un nombre dérivé et le définit comme « le quotient ultime de deux accroissements évanescents ».
Au XVIIIe siècle, Jean Le Rond d’Alembert (1717-1783) définit un nombre dérivé en utilisant explicitement la notion de taux d’accroissement. Joseph-Louis Lagrange (1736-1813) crée la notation f ’(x) pour désigner le nombre dérivé de la fonction f en x et propose d’appeler « dérivée de f » la fonction f ’.
Au XIXe siècle, Karl Weiertstrass (1815-1897) définit rigoureusement la dérivée d’une fonction numérique comme nous le faisons encore aujourd’hui, en utilisant le concept de limite créé par Augustin-Louis Cauchy (1789-1857).

Karl Weiertstrass (1815-1897)
2. Dérivées à droite et dérivées à gauche
Calcul approché de f ’(x) et de f ’’(x)
Une fonction numérique f est dérivable sur un intervalle si la courbe qui la représente admet une tangente et une seule en chacun des points de cet intervalle. On obtiendra une valeur approchée de la dérivée de f en identifiant localement la courbe à sa tangente.
1. Administration par un polynôme
Soit f une fonction numérique dérivable sur un intervalle ouvert I. Cherchons un polynôme P tel que P(x0)=f(x0), P’(x0)=f ’(x0) et, pour cela, posons P(x)=a+b(x-x0).
En faisant x=x0 dans l’expression de P, on obtient P(x0)=a d’où a=f(x0). En dérivant le polynôme P, on peut écrire P’(x)=b puis, en faisant x=x0 dans cette égalité, on obtient b=P’(x0) d’où b=f ’(x0). On a donc finalement P(x) = f(x0) + f ’(x0)(x- x0). On démontre qu’au voisinage de x0, f(x) ≈f(x0) + f ’(x0)(x - x0).
En fait, remplacer localement la fonction f par le polynôme P au voisinage de x0, revient à remplacer un petit arc de la courbe représentative de f par un petit segment de droite porté par la tangente à la courbe représentative de la fonction f au point d’abscisse x0. Le polynôme P est appelé développement de f(x) en série de Taylor6 au voisinage de x0 et à l’ordre 1.

Brook Taylor (1685-1731)
2. Calcul d’une valeur approchée de f ’(x)
Qu’est-ce qu’une équation différentielle ?
Les premières équations différentielles sont apparues au début du XVIIe siècle, avec la création du calcul infinitésimal et du calcul intégral. Elles ont d’abord servi à résoudre des problèmes de géométrie puis ont commencé à jouer un rôle important en mécanique. On peut les écrire de deux façons selon qu’on adopte les notations de Newton ou celles de Leibniz.
1. Historique
La première apparition des équations différentielles remonterait à l’année 1638 quand Florimond de Beaune (1601-1652), un mathématicien ami de René Descartes (1596-1650), proposa deux problèmes géométriques sur la construction d’une courbe connaissant une propriété de ses tangentes. Exprimé dans la langue d’aujourd’hui, le premier de ces deux problèmes est le suivant :
Soit C une courbe d’équation y=f(x) qui admet une tangente en chacun de ses points. Soit P[x;y)] un point quelconque de cette courbe et soit T la tangente en P à la courbe. T rencontre l’axe des x en A. La perpendiculaire à l’axe des x menée par P rencontre cet axe en H. Quel que soit P, la longueur du segment [AH] doit être constante. Construire la courbe C.
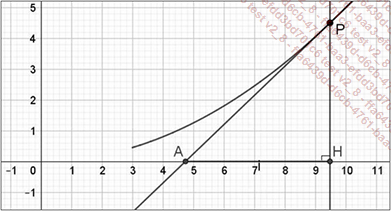
Résolvons ce problème avec les moyens d’aujourd’hui en choisissant un repère orthonormal. L’équation réduite de la tangente T est Y=f ’(x)(X-x)+f(x), relation dans laquelle f ’(x) représente la dérivée de f.
La méthode d’Euler
Soit y=f(x) une fonction numérique définie et dérivable sur un intervalle I qui est solution de l’équation différentielle du 1er ordre y’=F(x,y), F étant une fonction connue des variables x et y. On ne peut pas toujours calculer y explicitement, mais on peut calculer y(x) de façon approchée pour tout nombre x de l’intervalle I. Il existe différentes méthodes pour cela, la plus simple étant la méthode d’Euler (1707-1783).

Leonhard Euler (1707-1783)
1. Principe de la méthode d’Euler
Soit x0ϵI. Si la condition initiale y0=y(x0) est connue, on démontre que l’équation différentielle y’=F(x,y) admet généralement une solution unique8.
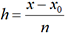 d’où xi = x0 + ih pour 0 ≤i≤n.
d’où xi = x0 + ih pour 0 ≤i≤n.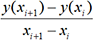 est une valeur approchée de y’(xi).
On peut alors écrire y(xi+1) = y(xi) + y’(xi)(xi+1 - xi) soit y(xi+1) = y(xi) + hy’(xi) pour
0 ≤ i ≤ n.
est une valeur approchée de y’(xi).
On peut alors écrire y(xi+1) = y(xi) + y’(xi)(xi+1 - xi) soit y(xi+1) = y(xi) + hy’(xi) pour
0 ≤ i ≤ n.Compte tenu de l’équation de départ, cette relation peut s’écrire y(xi+1) = y(xi) + h F(xi, y(xi)). Si on convient d’écrire yi au lieu de y(xi), l’égalité précédente s’écrit yi+1 = yi+ hy’ i pour...
Les méthodes de Runge-Kutta
Soit y=f(x) une fonction numérique définie et dérivable sur un intervalle I et soit F une fonction des variables x et y. Pour résoudre de façon approchée l’équation différentielle du 1er ordre y’=F(x,y), on peut utiliser la méthode de Runge-Kutta, plus performante que celle d’Euler.
1. Historique
Cette méthode de résolution approchée d’une équation différentielle a été proposée en 1901 par les deux mathématiciens allemands Carl Runge (1856-1927) et Martin Wilhem Kutta (1867-1944).
 Carl Runge (1856-1927) |
 Martin W. Kutta (1867-1944) |
2. Cas d’une équation différentielle du premier ordre
Comme dans le cas de la méthode proposée par Euler, il s’agit de construire une suite récurrence y’(i) qui approchera la solution cherchée y(x).
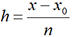 d’où xi = x0 + ih pour 0 ≤ i≤ n.
d’où xi = x0 + ih pour 0 ≤ i≤ n.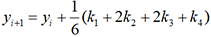 . Les nombres k1, k2, k3 et k4 sont
donnés par les formules
. Les nombres k1, k2, k3 et k4 sont
donnés par les formules 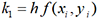 ,
, 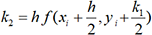 ,
, 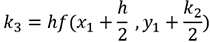 et k4 = h f(xi+h, yi+k3).
et k4 = h f(xi+h, yi+k3).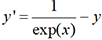 dont la
solution exacte est
dont la
solution exacte est 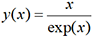 , avec les
conditions initiales x0=0
et y0=0.
, avec les
conditions initiales x0=0
et y0=0.# Méthode de Runge-Kutta... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

