Éléments de statistiques
Les paramètres d’une série statistique
Les observations d’une série statistique sont d’abord recueillies une à une au cours d’une enquête puis elles sont ensuite présentées dans une liste qui va faire l’objet d’un certain nombre de traitements.
1. Un exemple
Pour expliciter ces traitements, nous prendrons l’exemple d’une série de N notes, toutes comprises entre 0 et 20. Nous commencerons par ranger ces notes dans un ordre croissant en utilisant pour cela l’instruction sorted(liste).
# Rangement des notes de la série dans un ordre croissant
série=[11,8,17,12,11,6,11,10,12,15,8,8,9,8,11,15,5,5,9,12,13,11,
8, 7,5,12,13,13]
N=len(série)
sérieclassée=sorted(série)
print(sérieclassée)
# Note la plus basse, note la plus élevée et étendue de la série
print("note la plus basse :",sérieclassée[0])
print("note la plus haute :", sérieclassée[N-1])
print("étendue de la série :", sérieclassée[N-1]-sérieclassée[0]) Voici le résultat :
[5, 5, 5, 6, 7, 8, 8, 8, 8, 8, 9, 9, 10, 11, 11, 11, 11, 11, 12,
12, 12, 12, 13, 13, 13, 15, 15, 17]
note la plus basse : 5
note la plus haute : 17
étendue de la série : 12 2. Construction du tableau des effectifs
Une fois que la série des notes a été rangée dans un ordre croissant, on peut construire le tableau des effectifs de la série. Dans le programme qui effectue ce travail, on utilise 3 listes et 4 instructions particulières de Python qui permettent d’agir sur ces listes. L’instruction liste.count(y) détermine dans une liste le rang de la note y. L’instruction if liste[i]not in copie détermine...
Covariance et coefficient de corrélation
En statistique, il est fréquent d’observer conjointement deux caractères statistiques pour déterminer s’ils sont indépendants ou si, au contraire, il existe une corrélation entre eux.
1. Historique
Soit x1, x2, x3, ......., xn et y1, y2, y3, ....., yn deux séries statistiques de n éléments chacune de moyennes mx et my, de variances Vx et Vy. On peut représenter graphiquement ces deux séries par un nuage de points en prenant xi et yi pour coordonnées du point Mi. Prenons par exemple 2, 3, 3, 5, 7, 12, 15 comme série des x et 1, 4, 3, 7, 10, 12, 15 comme série des y :
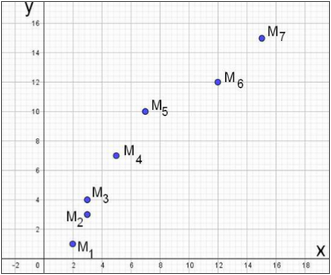
Les 7 points ne semblent pas disposés au hasard et il semble y avoir une certaine « corrélation » entre les deux séries. La notion de corrélation provient de la biologie. Selon le grand naturaliste Cuvier, il existe nécessairement des corrélations entre les différentes parties du corps d’un animal. Selon lui, ces corrélations peuvent concourir à adapter une espèce à un milieu ou à un régime alimentaire précis ou, au contraire, n’avoir aucune utilité en tant que telles.
La notion a été introduite en statistique par Francis Galton (1822-1911), un cousin de Charles Darwin (1809-1882). Elle a été mathématisée par le mathématicien britannique Karl Pearson (1857-1936) en 1896.
2. Définitions
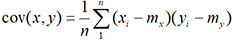 .
.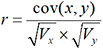 . On démontre que ce coefficient varie
entre -1 et +1. Son interprétation est la suivante :
. On démontre que ce coefficient varie
entre -1 et +1. Son interprétation est la suivante :-
S’il est proche de 0, on peut considérer...
Ajustements linéaires et autres
Soit (xn) et (yn) deux séries statistiques formées de nombres. La méthode des moindres carrés permet de choisir une fonction f continue dont la courbe représentative s’ajuste le mieux possible aux points qui représentent les 2 séries.
1. Historique
La méthode des moindres carrés a été élaborée par Gauss (1777-1855) et par Legendre (1752-1833) au début du XIXe siècle dans le cadre de leurs travaux de mécanique céleste. Elle permet de rechercher une fonction qui puisse rendre compte des données expérimentales obtenues lors de mesures généralement entachées d’erreurs.
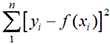 .
.2. Ajustement linéaire
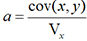 et b = my - amx pour
réaliser le meilleur ajustement possible.
et b = my - amx pour
réaliser le meilleur ajustement possible.# Ajustement linéaire
from math import*
n=eval(input("Quel est l'effectif de chaque série ?"))
listex,listey=[],[]
# Calcul des moyennes et des variances
sommex,sommey=0,0
for i in range (1,n+1):
x=eval(input("Valeur de x ?"))
listex=listex+[x]
sommex=sommex+x
for i in range (1,n+1):
y=eval(input("Valeur de y ?"))
listey=listey+[y]
sommey=sommey+y
mx,my=sommex/n,sommey/n
v,w=0,0
for i in range(0,n):
v=v+(mx-listex[i])**2
w=w+(my-listey[i])**2
Vx,Vy=v/n,w/n
# Calcul... Editions ENI Livres | Vidéos | e-Formations
Editions ENI Livres | Vidéos | e-Formations

